Advertisements
Advertisements
प्रश्न
समद्विबाहु ΔABC में AB = AC है। BD तथा CE दो माध्यिकाएँ हैं तो सिद्ध कीजिए कि BD = CE
उत्तर

बिंदु D रेख AC का मध्यबिंदु है । ...(मध्यबिंदु की परिभाषा से)
∴ AD = DC = `1/2` AC ...(1)
AE = EB = `1/2`AB ....(2)
AB = AC
दोनों पक्षो में `1/2` से गुणा करने पर,
`1/2 "AB" = 1/2 "AC"` ...(3)
∴ AE = AD .....[(1), (2) तथा (3) से] ...(4)
ΔBAD तथा ΔCAE में,
रेख AB ≅ रेख AC ...(दिया है।)
∠BAD ≅ ∠CAE ...(सामान्य रूप)
रेख AE ≅ रेख AD ....(4 से)
∴ ΔBAD ≅ ΔCAE ....(सर्वांगसमता की भू - को - भू कसौटी से)
∴ रेख BD ≅ रेख CE
∴ BD = CE.
APPEARS IN
संबंधित प्रश्न
यदि △DEF ≅ △BCA हो, तो △BCA के उन भागो को लिखिए जो ∠E के संगत हो:
∆ABC में, ∠A = 30°, ∠B = 40° और ∠C = 110°, ∆PQR में, ∠P = 30° ∠Q = 40° और ∠R = 110° एक विद्यार्थी कहता है कि A.A.A. सर्वांगसमता प्रतिबन्ध से ∆ABC ≅ ∆PQR है। क्या यह कथन सत्य है? क्यों या क्यों नहीं?
एक वर्गांकित शीट पर, बराबर क्षेत्रफलों वाले दो त्रिभुजों को इस प्रकार बनाइए कि त्रिभुज सर्वांगसम हों
आप उनके परिमाप के बारे में क्या कह सकते हैं?
एक वर्गांकित शीट पर, बराबर क्षेत्रफलों वाले दो त्रिभुजों को इस प्रकार बनाइए कि त्रिभुज सर्वांगसम न हों।
आप उनके परिमाप के बारे में क्या कह सकते हैं?
∆ABC में, BC = AB और ∠B = 80° है, तब ∠A बराबर है
∆PQR में, ∠R = ∠P तथा QR = 4 cm और PR = 5 cm है, तब PQ की लम्बाई है
त्रिभुजों ABC और PQR में, AB = AC, ∠C = ∠P और ∠B = ∠Q है। ये दोनों त्रिभुज हैं
निम्नलिखित आकृति में, D और E त्रिभुज ABC की भुजा BC पर दो बिंदु इस प्रकार स्थित हैं कि BD = CE और AD = AE है। दर्शाइए कि ∆ABD ≅ ∆ACE है।
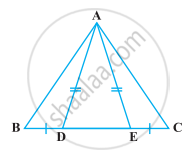
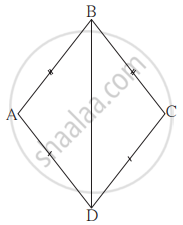
आकृति में रेख AB ≅ रेख BC तथा रेख AD ≅ रेख CD तो सिद्ध कीजिए Δ ABD ≅ Δ CBD
ΔTPQ में ∠T = 65°, ∠P = 95° तो निम्नलिखित में से कौन-सा कथन सत्य है ?
