Advertisements
Advertisements
प्रश्न
निचे दी गई आकृति के आधार पर ΔPQR में यदि PQ > PR तथा ∠Q तथा ∠R के समद्विभाजक बिंदु S पर प्रतिच्छेदित करते हैं तो सिद्ध कीजिए कि SQ > SR

उत्तर
दत्त : ∆ PQR में, PQ > PR और ∠Q और ∠R के समद्विभाजक S पर प्रतिच्छेदित करते हैं।
साध्य : SQ > SR
उपपत्ति :
∠SQR = `1/2` ∠PQR ….(i) ...[किरण QS ∠PQR को समद्विभाजित करती है]
∠SRQ = `1/2` ∠PRQ ...(ii) ...[किरण RS ∠PRQ को समद्विभाजित करती है]
∆ PQR में,
PQ > PR ...(दिया है।)
∴ ∠R > ∠Q ....[बड़ी भुजा के विपरीत कोण बड़ा होता है।]
∴ `1/2 ("∠R") > 1/2 ("∠Q") ...["दोनों पक्षों को" 1/2"से गुणा करने पर"] `
∴ ∠SRQ > ∠SQR ...(iii) ...[(i) तथा (ii) से]
∆SQR में,
∠SRQ > ∠SQR ...[(iii) से]
∴ SQ > SR ... [बड़े कोण के विपरीत भुजा बड़ी होती है]
APPEARS IN
संबंधित प्रश्न
ΔMNP में रेख NQ यह ∠N की समद्विभाजक है। यदि MN = 5, PN = 7, MQ = 2.5 तो QP का मान ज्ञात कीजिए।
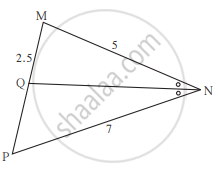
आकृति में दी गई जानकारी के आधार पर QP का मान ज्ञात कीजिए।
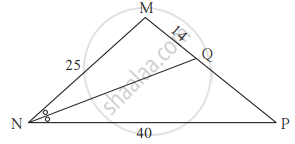
ΔLMN में किरण MT यह ∠LMN की समद्विभाजक है। LM = 6, MN = 10, TN = 8 तो LT का मान ज्ञात कीजिए।
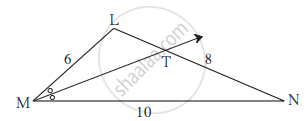
ΔABC में रेख BD यह ∠ABC की समद्विभाजक है, यदि AB = x, BC = x + 5, AD = x – 2, DC = x + 2 तो x का मान ज्ञात कीजिए।
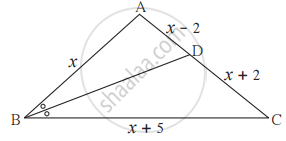
ΔABC में AB = AC, ∠B तथा ∠C के समद्विभाजक भुजा AC तथा भुजा AB को क्रमश: बिंदु D तथा E पर प्रतिच्छेदित करते हैं। तो सिद्ध कीजिए कि रेख ED || रेख BC
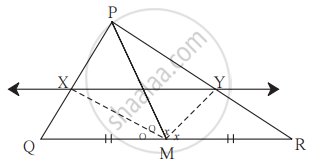
ΔPQR में रेख PM माध्यिका है। ∠PMQ तथा ∠PMR के समद्विभाजक भुजा PQ तथा भुजा PR को क्रमश: बिंदु X और बिंदु Y पर प्रतिच्छेदित करते हैं, तो सिद्ध कीजिए कि, XY || QR.
दिए गए रिक्त स्थानों को भरकर उपपत्ति पूर्ण कीजिए।
ΔPMQ में किरण MX यह ∠PMQ की समद्विभाजक है।
∴ `square/square = square/square` ........(I) (कोण समद्विभाजक प्रमेय)
ΔPMR में किरण MY यह ∠PMR की समद्विभाजक है।
∴ `square/square = square/square` ........(II) (कोण समद्विभाजक प्रमेय)
परंतु `"MP"/"MQ" = "MP"/"MR"` ................ (बिंदु M यह QR का मध्य बिंदु है अर्थात MQ = MR)
∴ `"PX"/"XQ" = "PY"/"YR"`
∴ XY || QR ............(समानुपात के मूलभूत प्रमेय का विलोम)
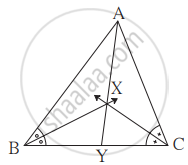
आकृति ΔABC में ∠B तथा ∠C के समद्विभाजक परस्पर एक दूसरे को बिंदु X पर प्रतिच्छेदित करते हैं। रेखा AX यह भुजा BC को बिंदु Y पर प्रतिच्छेदित करती है; यदि AB = 5, AC = 4, BC = 6 तो `"AX"/"XY"` का मान ज्ञात कीजिए।
निचे दी गई आकृति के आधार पर ∠RST = 56°, रेख PT ⊥ किरण ST, रेख PR ⊥ किरण SR तथा रेख PR ≅ रेख PT हो तो ∠RSP का माप ज्ञात कीजिए। कारणसहित लिखिए।

ΔABC में ∠BAC की समद्विभाजक भुजा BC पर लंब हो तो सिद्ध कीजिए कि D ABC समद्विबाहु त्रिभुज है।

ΔABC में, किरण BD यह ∠ABC का कोण समद्विभाजक है। A - D - C, रेख DE || भुजा BC, A - E - B हो, तो सिद्ध कीजिए `("AB")/("BC") = ("AE")/("EB")`
उपपत्ति:
ΔABC में, किरण BD यह ∠B को समद्विभाजित करता है।
∴ `square/("BC") = ("AD")/("DC")` ......(I) (`square`)
ΔABC में, DE || BC
∴ `(square)/("EB") = ("AD")/("DC")` ....(II) (`square`)
∴ `("AB")/square = square/("EB")` [(I) व (II) से]
