Advertisements
Advertisements
प्रश्न
त्रिभुजों ABC और PQR में, AB = AC, ∠C = ∠P और ∠B = ∠Q है। ये दोनों त्रिभुज हैं
विकल्प
समद्विबाहु परंतु सर्वांगसम नहीं
समद्विबाहु और सर्वांगसम
सर्वांगसम परंतु समद्विबाहु नहीं
न तो सर्वांगसम और न ही समद्विबाहु
उत्तर
समद्विबाहु परंतु सर्वांगसम नहीं
स्पष्टीकरण -
त्रिभुज ABC में,
AB = AC ...[दिया गया है।]
∠C = ∠B ...[समान भुजाओं के सम्मुख कोण बराबर होते हैं।]
इसलिए, त्रिभुज ABC में एक समद्विबाहु त्रिभुज है।
∠B = ∠Q ...[दिया गया है।]
∠C = ∠P
∠P = ∠Q ...[चूँकि, ∠C = ∠B]
QR = PR ...[समान कोणों की सम्मुख भुजाएँ बराबर होती हैं।]
इसलिए, त्रिभुज में PQR भी एक समद्विबाहु त्रिभुज है।

अतः, दोनों त्रिभुज समद्विबाहु हैं लेकिन सर्वांगसम नहीं हैं।
APPEARS IN
संबंधित प्रश्न
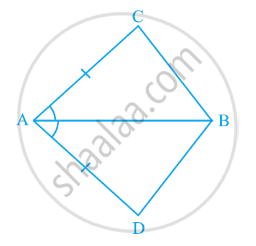
चतुर्भुज ABCD में, AC = AD है और AB, कोण A को समद्विभाजित करता है (देखिए आकृति)। दर्शाइए कि △ABC ≌ △ABD है। BC और BD के बारे में आप क्या कह सकते हैं?
यदि सुमेलन ABC ↔ FED के अंतर्गत △ABC ≅ △FED तो त्रिभुजो के सभी संगत सर्वागसम भागो को लिखिए।
यदि △DEF ≅ △BCA हो, तो △BCA के उन भागो को लिखिए जो ∠E के संगत हो:
यदि △DEF ≅ △BCA हो, तो △BCA के उन भागो को लिखिए जो ∠F के संगत हो:
∆ABC में, ∠A = 30°, ∠B = 40° और ∠C = 110°, ∆PQR में, ∠P = 30° ∠Q = 40° और ∠R = 110° एक विद्यार्थी कहता है कि A.A.A. सर्वांगसमता प्रतिबन्ध से ∆ABC ≅ ∆PQR है। क्या यह कथन सत्य है? क्यों या क्यों नहीं?
निम्नलिखित में से कौन त्रिभुजों की सर्वांगसमता की एक कसौटी नहीं है?
∆ABC में, BC = AB और ∠B = 80° है, तब ∠A बराबर है
∆PQR में, ∠R = ∠P तथा QR = 4 cm और PR = 5 cm है, तब PQ की लम्बाई है
नीचे दिए गए त्रिभुज की जोड़िय में दर्शाई गई जानकारी का निरीक्षण कीजिए । वे त्रिभुज किस कसौटी के आधार पर सर्वांगसम हैं । शेष सर्वांगसम घटक भी लिखिए ।
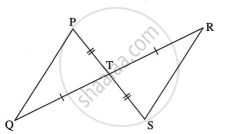
आकृति में दर्शाई गई जानकारी के आधार पर,
ΔPTQ तथा ΔSTR में
रेख PT ≅ रेख ST
∠PTQ ≅ ∠STR ...शीर्षाभिमुख कोण
रेख TQ ≅ रेख TR
∴ ΔPTQ ≅ ΔSTR .... `square` कसौटी
∴ `{:(∠"TPQ" ≅ square),(व square ≅ ∠"TRS"):}}` ...सर्वांगसम त्रिभुज के संगत कोण
रेख PQ ≅ `square` ...सर्वांगसम त्रिभुज की संगत भुजाएँ
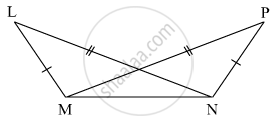
नीचे दी गई आकृति में दर्शाए अनुसार ΔLMN तथा ΔPNM में LM = PN, LN = PM हो तो त्रिभुजों की सर्वांगसमता की कसौटी लिखिए । शेष सर्वांगसम घटकों के नाम भी लिखिए ।