Advertisements
Advertisements
प्रश्न
निम्नलिखित में से कौन त्रिभुजों की सर्वांगसमता की एक कसौटी नहीं है?
विकल्प
SAS
ASA
SSA
SSS
उत्तर
SSA
स्पष्टीकरण -
हम वह जानते हैं,
दो त्रिभुज सर्वांगसम होते हैं, यदि एक त्रिभुज की भुजा (S) और कोण (A) दूसरे कोण के बराबर हों।
और त्रिभुज की सर्वांगसमता के मानदंड SAS, ASA, SSS और RHS हैं।
SSA त्रिभुज की सर्वांगसमता की कसौटी नहीं है।
APPEARS IN
संबंधित प्रश्न
यदि सुमेलन ABC ↔ FED के अंतर्गत △ABC ≅ △FED तो त्रिभुजो के सभी संगत सर्वागसम भागो को लिखिए।
यदि △DEF ≅ △BCA हो, तो △BCA के उन भागो को लिखिए जो ∠F के संगत हो:
यदि △DEF ≅ △BCA हो, तो △BCA के उन भागो को लिखिए जो `bar(DF)` के संगत हो:
एक वर्गांकित शीट पर, बराबर क्षेत्रफलों वाले दो त्रिभुजों को इस प्रकार बनाइए कि त्रिभुज सर्वांगसम हों
आप उनके परिमाप के बारे में क्या कह सकते हैं?
यदि AB = QR, BC = PR और CA = PQ है, तो ______।
त्रिभुजों ABC और PQR में, AB = AC, ∠C = ∠P और ∠B = ∠Q है। ये दोनों त्रिभुज हैं
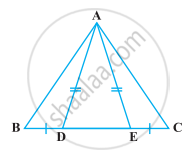
निम्नलिखित आकृति में, D और E त्रिभुज ABC की भुजा BC पर दो बिंदु इस प्रकार स्थित हैं कि BD = CE और AD = AE है। दर्शाइए कि ∆ABD ≅ ∆ACE है।
नीचे दिए गए उदाहरण में त्रिभुज की जोड़ियों के सर्वांगसम घटक एक जैसे चिह्न से दर्शाए गए हैं। प्रत्येक जोड़ी के त्रिभुज किस कसौटी के आधार पर सर्वांगसम हैं रिक्त स्थानों में वह कसौटी लिखिए।
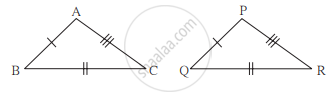
______ कसौटी से
ΔABC ≅ ΔPQR
नीचे दिए गए प्रत्येक उदाहरण में त्रिभुज की जोड़ि के सर्वांगसम घटक एक जैसे चिह्न से दर्शाए गए हैं। त्रिभुज किस कसौटी के आधार पर सर्वांगसम हैं रिक्त स्थानों में वह कसौटी लिखिए।
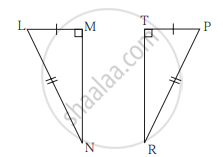
______ कसौटी से
ΔLMN ≅ ΔPTR
नीचे दी गई आकृति में दर्शाए अनुसार ΔLMN तथा ΔPNM में LM = PN, LN = PM हो तो त्रिभुजों की सर्वांगसमता की कसौटी लिखिए । शेष सर्वांगसम घटकों के नाम भी लिखिए ।