Advertisements
Advertisements
प्रश्न
यदि AB = QR, BC = PR और CA = PQ है, तो ______।
विकल्प
∆ABC ≅ ∆PQR
∆CBA ≅ ∆PRQ
∆BAC ≅ ∆RPQ
∆PQR ≅ ∆BCA
उत्तर
यदि AB = QR, BC = PR और CA = PQ है, तो ∆CBA ≅ ∆PRQ।
स्पष्टीकरण -
हम जानते हैं कि, यदि ΔRST, ΔUVW के सर्वांगसम है, अर्थात, ΔRST = ΔUVW, तो ΔRST की भुजाएँ ΔUVW की संगत समान भुजाओं पर पड़ती हैं और ΔRST के कोण ΔUVW के संगत समान कोणों पर गिरते हैं।
यहाँ, AB = QR, BC = PR और CA = PQ दिया है, जो दर्शाता है कि AB, QR को कवर करता है, BC, PR को कवर करता है और CA, PQ को कवर करता है, अर्थात, A, Q के संगत है। B, R के संगत है और C, P के संगत है।
या A ↔ Q, B ↔ R, C ↔ P
इस पत्राचार के अंतर्गत,
ΔABC ≅ ΔQRP, इसलिए विकल्प (a) गलत है,
or ΔCBA ≅ ΔPRQ, इसलिए विकल्प (b) सही है,
or ΔBAC ≅ ΔRQP, इसलिए विकल्प (c) गलत है,
or ΔBCA ≅ ΔRPQ, इसलिए विकल्प (d) गलत है।
APPEARS IN
संबंधित प्रश्न
यदि सुमेलन ABC ↔ FED के अंतर्गत △ABC ≅ △FED तो त्रिभुजो के सभी संगत सर्वागसम भागो को लिखिए।
यदि △DEF ≅ △BCA हो, तो △BCA के उन भागो को लिखिए जो ∠E के संगत हो:
कथनों को पूरा कीजिए:
ΔBCA ≅?
∆QRS ≅ ?
∆ABC में, BC = AB और ∠B = 80° है, तब ∠A बराबर है
∆PQR में, ∠R = ∠P तथा QR = 4 cm और PR = 5 cm है, तब PQ की लम्बाई है
∆PQR में, यदि ∠R > ∠Q है, तो ______
नीचे दिए गए उदाहरण में त्रिभुजों की जोड़ि के सर्वांगसम घटक एक जैसे चिह्न से दर्शाए गए हैं जोड़ी के त्रिभुज किस कसौटी के आधार पर सर्वांगसम हैं रिक्त स्थानों में वह कसौटी लिखिए।
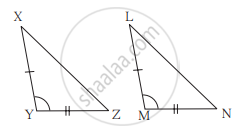
______ कसौटी से
ΔXYZ ≅ ΔLMN
नीचे दी गई आकृति में Δ ABC तथा Δ PQR की सर्वांगसमता की कसौटी लिखकर शेष सर्वांगसम घटकों के नाम लिखिए।
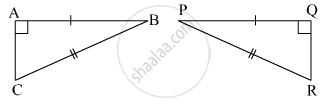
निचे दी गई आकृति के आधार पर ∠P ≅ ∠R, रेख PQ ≅ रेख QR, तो सिद्ध कीजिए कि, ΔPQT ≅ ΔRQT
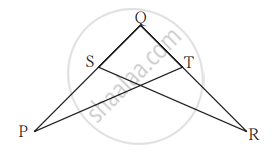
ΔTPQ में ∠T = 65°, ∠P = 95° तो निम्नलिखित में से कौन-सा कथन सत्य है ?
