Advertisements
Advertisements
प्रश्न
नीचे दिए गए उदाहरण में त्रिभुजों की जोड़ि के सर्वांगसम घटक एक जैसे चिह्न से दर्शाए गए हैं जोड़ी के त्रिभुज किस कसौटी के आधार पर सर्वांगसम हैं रिक्त स्थानों में वह कसौटी लिखिए।
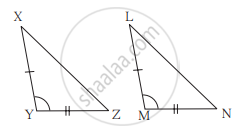
______ कसौटी से
ΔXYZ ≅ ΔLMN
उत्तर
भु - को - भु कसौटी से
APPEARS IN
संबंधित प्रश्न
चतुर्भुज ABCD में, AC = AD है और AB, कोण A को समद्विभाजित करता है (देखिए आकृति)। दर्शाइए कि △ABC ≌ △ABD है। BC और BD के बारे में आप क्या कह सकते हैं?
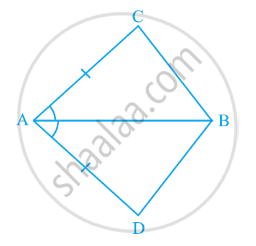
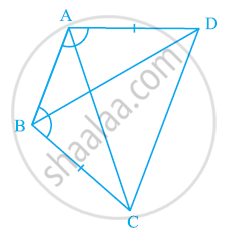
ABCD एक चतुर्भुज है, जिसमें AD = BC और ∠DAB = ∠CBA है (देखिए आकृति)। सिद्ध कीजिए कि:
- △ABD ≌ △BAC
- BD = AC
- ∠ABD = ∠BAC
यदि △DEF ≅ △BCA हो, तो △BCA के उन भागो को लिखिए जो `bar(DF)` के संगत हो:
∆ABC में, ∠A = 30°, ∠B = 40° और ∠C = 110°, ∆PQR में, ∠P = 30° ∠Q = 40° और ∠R = 110° एक विद्यार्थी कहता है कि A.A.A. सर्वांगसमता प्रतिबन्ध से ∆ABC ≅ ∆PQR है। क्या यह कथन सत्य है? क्यों या क्यों नहीं?
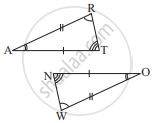
आकृति में दो त्रिभुज ART तथा OWN सर्वांगसम हैं जिसके संगत भागो को अंकित किया गया है। हम लिख सकते है △RAT ≅ ?
∆ABC में, BC = AB और ∠B = 80° है, तब ∠A बराबर है
∆PQR में, यदि ∠R > ∠Q है, तो ______
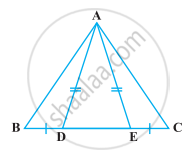
निम्नलिखित आकृति में, D और E त्रिभुज ABC की भुजा BC पर दो बिंदु इस प्रकार स्थित हैं कि BD = CE और AD = AE है। दर्शाइए कि ∆ABD ≅ ∆ACE है।
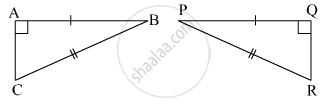
नीचे दी गई आकृति में Δ ABC तथा Δ PQR की सर्वांगसमता की कसौटी लिखकर शेष सर्वांगसम घटकों के नाम लिखिए।
आकृति में रेख AB ≅ रेख BC तथा रेख AD ≅ रेख CD तो सिद्ध कीजिए Δ ABD ≅ Δ CBD