Advertisements
Advertisements
प्रश्न
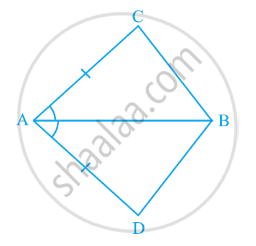
चतुर्भुज ABCD में, AC = AD है और AB, कोण A को समद्विभाजित करता है (देखिए आकृति)। दर्शाइए कि △ABC ≌ △ABD है। BC और BD के बारे में आप क्या कह सकते हैं?
उत्तर
दिया है: चतुर्भुज ABCD में, AC = AD और AB, ∠A को समद्विभाजित करता है।
सिद्ध करना है: △ABC ≌ △ABD
उपपत्ति: △ABC और △ABD में,
AC = AD ...[दिया है]
∠BAC = ∠BAD ...[∵ AB, ∠A को समद्विभाजित करता है। दिया है]
AB = AB ...[उभयनिष्ठ]
∴ △ABC ≌ △ABD ...[SAS सर्वांगसमता नियम द्वारा]
अत: BC = BD ...[सर्वांगसम त्रिभुजों के संगत भाग]
APPEARS IN
संबंधित प्रश्न
यदि △DEF ≅ △BCA हो, तो △BCA के उन भागो को लिखिए जो ∠E के संगत हो:
यदि △DEF ≅ △BCA हो, तो △BCA के उन भागो को लिखिए जो `barEF` के संगत हो:
∆ABC में, ∠A = 30°, ∠B = 40° और ∠C = 110°, ∆PQR में, ∠P = 30° ∠Q = 40° और ∠R = 110° एक विद्यार्थी कहता है कि A.A.A. सर्वांगसमता प्रतिबन्ध से ∆ABC ≅ ∆PQR है। क्या यह कथन सत्य है? क्यों या क्यों नहीं?
कथनों को पूरा कीजिए:
ΔBCA ≅?
∆QRS ≅ ?
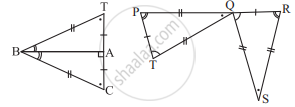
एक वर्गांकित शीट पर, बराबर क्षेत्रफलों वाले दो त्रिभुजों को इस प्रकार बनाइए कि त्रिभुज सर्वांगसम हों
आप उनके परिमाप के बारे में क्या कह सकते हैं?
यदि AB = QR, BC = PR और CA = PQ है, तो ______।
∆ABC में, AB = AC और ∠B = 50° है, तब ∠C बराबर है
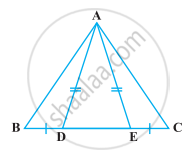
निम्नलिखित आकृति में, D और E त्रिभुज ABC की भुजा BC पर दो बिंदु इस प्रकार स्थित हैं कि BD = CE और AD = AE है। दर्शाइए कि ∆ABD ≅ ∆ACE है।
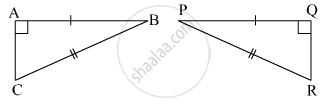
नीचे दी गई आकृति में Δ ABC तथा Δ PQR की सर्वांगसमता की कसौटी लिखकर शेष सर्वांगसम घटकों के नाम लिखिए।
समद्विबाहु ΔABC में AB = AC है। BD तथा CE दो माध्यिकाएँ हैं तो सिद्ध कीजिए कि BD = CE
