Advertisements
Advertisements
प्रश्न
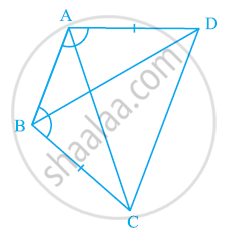
ABCD एक चतुर्भुज है, जिसमें AD = BC और ∠DAB = ∠CBA है (देखिए आकृति)। सिद्ध कीजिए कि:
- △ABD ≌ △BAC
- BD = AC
- ∠ABD = ∠BAC
उत्तर
चतुर्भुज ABCD में,
AD = BC और ∠DAB = ∠CBA
i. ΔABD और ΔBAC में,
AD = BC ...[दिया गया है।]
∠DAB = ∠CBA ...[दिया गया है।]
AB = BA ...[उभयनिष्ठ]
∴ ΔABD ≅ ΔBAC ...[SAS सर्वांगसमता द्वारा]
ii. चूँकि, ΔABD ≅ ΔBAC
BD = AC ...[सर्वांगसम त्रिभुजों के संगत भागों द्वारा]
iii. चूँकि, ΔABD ≅ ΔBAC
∠ABD = ∠BAC ...[सर्वांगसम त्रिभुजों के संगत भागों द्वारा]
APPEARS IN
संबंधित प्रश्न
यदि △DEF ≅ △BCA हो, तो △BCA के उन भागो को लिखिए जो `barEF` के संगत हो:
निम्नलिखित में से कौन त्रिभुजों की सर्वांगसमता की एक कसौटी नहीं है?
यदि AB = QR, BC = PR और CA = PQ है, तो ______।
∆ABC में, AB = AC और ∠B = 50° है, तब ∠C बराबर है
∆ABC में, BC = AB और ∠B = 80° है, तब ∠A बराबर है
एक त्रिभुज की दो भुजाओं की लंबाइयाँ 5 cm और 1.5 cm हैं। इस त्रिभुज की तीसरी भुजा की लंबाई निम्नलिखित नहीं हो सकती ______
नीचे दिए गए उदाहरण में त्रिभुज की जोड़ियों के सर्वांगसम घटक एक जैसे चिह्न से दर्शाए गए हैं। प्रत्येक जोड़ी के त्रिभुज किस कसौटी के आधार पर सर्वांगसम हैं रिक्त स्थानों में वह कसौटी लिखिए।
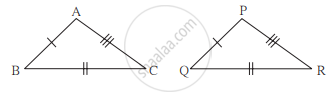
______ कसौटी से
ΔABC ≅ ΔPQR
नीचे दिए गए उदाहरण में त्रिभुजों की जोड़ि के सर्वांगसम घटक एक जैसे चिह्न से दर्शाए गए हैं जोड़ी के त्रिभुज किस कसौटी के आधार पर सर्वांगसम हैं रिक्त स्थानों में वह कसौटी लिखिए।
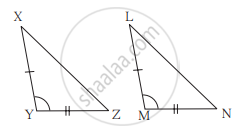
______ कसौटी से
ΔXYZ ≅ ΔLMN
नीचे दिए गए प्रत्येक उदाहरण में त्रिभुज की जोड़ि के सर्वांगसम घटक एक जैसे चिह्न से दर्शाए गए हैं। त्रिभुज किस कसौटी के आधार पर सर्वांगसम हैं रिक्त स्थानों में वह कसौटी लिखिए।
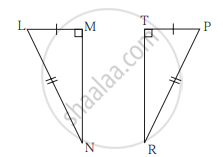
______ कसौटी से
ΔLMN ≅ ΔPTR
ΔTPQ में ∠T = 65°, ∠P = 95° तो निम्नलिखित में से कौन-सा कथन सत्य है ?
