Advertisements
Advertisements
Question
Expand: (2a – 3b)2
Solution
(2a – 3b)2
Using the identity (x - y)2 = x2 - 2xy + y2
(2a - 3b)2 = (2a)2 - 2 × 2a × (3b)2
= 4a2 - 12ab + 9b2
APPEARS IN
RELATED QUESTIONS
Use a suitable identity to get the following products.
`(3a - 1/2)(3a - 1/2)`
Using identities, evaluate 297 × 303
Using identities, evaluate 78 × 82
Using identities, evaluate 8.92
Simplify: (a + b)2 + (a – b)2
(a + b)2 = a2 + b2
Factorise the following, using the identity a2 + 2ab + b2 = (a + b)2.
x2 + 12x + 36
Factorise the following, using the identity a2 + 2ab + b2 = (a + b)2.
4x2 + 4x + 1
Verify the following:
(7p – 13q)2 + 364pq = (7p + 13q)2
Take suitable number of cards given in the adjoining diagram [G(x × x) representing x2, R(x × 1) representing x and Y(1 × 1) representing 1] to factorise the following expressions, by arranging the cards in the form of rectangles:
- 2x2 + 6x + 4
- x2 + 4x + 4.
Factorise 2x2 + 6x + 4 by using the figure.
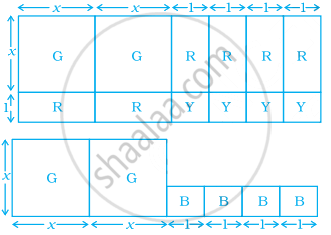
Calculate the area of figure.
