Advertisements
Advertisements
Question
Fig. shows a uniform meter scale weighing 100 N pivoted at its centre. Two weights of 500 N and 300 N are hung from the ruler as shown in fig.

(i) Calculate total clockwise and anticlockwise moments.
(ii) Calculate difference in clockwise moment and anticlockwise moment.
(iii) Calculate the distance from O where a 100 N weight should be suspended to balance the meter scale.
Solution
Let the weight 500 N be hung from the 40cm mark and the weight 300N be hung from the 80 cm mark
(i) Then, total clockwise moment = 500 x (50 - 40) = 500 x 10 = 5000 Nm
Total anticlockwise moment = 300 x (80 - 50) = 300 x 30 = 9000 Nm
(ii) Difference in clockwise and anticlockwise moment = 9000 - 5000 = 4000Nm
(iii) Let the 100 N weight be hung at a distance 'd' from the point 'o' to its left
Then,total clockwise moment = 5000 + 100 d
In balanced condition, sum of clockwise moments = sum of anticlockwise moments
5000 + 100 d = 9000
or 100 d = 4000
or d = 40cm
the weight 100 N should be a hung from the 40cm mark so as to balance the scale.
APPEARS IN
RELATED QUESTIONS
A half metre rod is pivoted at the centre with two weights of 20gf and 12gf suspended at a perpendicular distance of 6 cm and 10 cm from the pivot respectively as shown below.
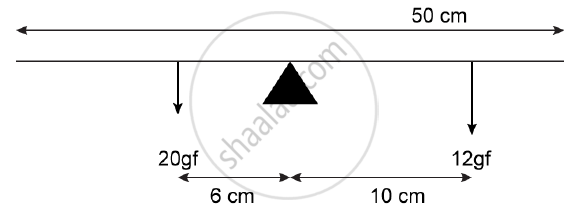
1) Which of the two forces acting on the rigid rod causes clockwise moment?
2) Is the rod in equilibrium?
3) The direction of 20 kgf force is reversed. What is the magnitude of the resultant moment of the forces on the rod?
Define force. State its S.I. unit.
How does the effect of force differ when it is applied on a non-rigid body?
State the S.I. unit of moment of force.
What is thrust?
State two factor on which moment of force about a point depends.
Define couple.
State two factors on which moment of the force about a point depends.
State the units of moment of force.
Calculate the minimum distance between point of application of force and axis of rotation of a rigid body, if a force 125 N produces a moment of force of 25.75 Nm.
