Advertisements
Advertisements
Question
Fill in the blanks :
Negation of “some men are animal” is –––––––––.
Solution
Negation of “some men are animal” is No men are animals.
APPEARS IN
RELATED QUESTIONS
Write the following compound statement symbolically.
Nagpur is in Maharashtra and Chennai is in Tamil Nadu.
Construct the truth table of the following statement pattern.
(p ∧ ∼q) ↔ (p → q)
Construct the truth table of the following:
p → (q → p)
Determine the truth values of p and q in the following case:
(p ∨ q) is T and (p ∧ q) is T
Determine the truth values of p and q in the following case:
(p ∨ q) is T and (p ∨ q) → q is F
Express the following statement in symbolic form.
e is a vowel or 2 + 3 = 5
Write the truth value of the negation of the following statement.
For every x ∈ N, x + 3 < 8.
Write the following statement in symbolic form.
If triangle is equilateral then it is equiangular.
Write the following statement in symbolic form.
It is not true that “i” is a real number.
If p and q are true and r and s are false, find the truth value of the following compound statement.
p ∧ (q ∧ r)
State whether the following statement is True or False:
The negation of 10 + 20 = 30 is, it is false that 10 + 20 ≠ 30.
Assuming the first statement p and second as q. Write the following statement in symbolic form.
The necessary condition for existence of a tangent to the curve of the function is continuity.
Assuming the first statement p and second as q. Write the following statement in symbolic form.
To be brave is necessary and sufficient condition to climb the Mount Everest.
Assuming the first statement p and second as q. Write the following statement in symbolic form.
If a real number is not rational, then it must be irrational.
If p : Proof is lengthy.
q : It is interesting.
Express the following statement in symbolic form.
Proof is lengthy and it is not interesting.
If p : Proof is lengthy.
q : It is interesting.
Express the following statement in symbolic form.
It is not true that the proof is lengthy but it is interesting.
Let p : Sachin wins the match.
q : Sachin is a member of Rajya Sabha.
r : Sachin is happy.
Write the verbal statement of the following.
(p ∧ q) ∨ r
Let p : Sachin wins the match.
q : Sachin is a member of Rajya Sabha.
r : Sachin is happy.
Write the verbal statement of the following.
p → q
Write the negation of the following.
Kanchanganga is in India and Everest is in Nepal.
Write the negation of the following statement.
∀ n ∈ N, n + 3 > 9.
The negation of the statement (p ˄ q) `→` (r ˅ ∼ p) is ______.
Negation of “Some men are animal “ is ______
Given 'p' and 'q' as true and 'r' as false, the truth values of p v (q ∧ ~r) and (p → r) ∧ q are respectively
If p, q are true statement and r is false statement, then which of the following statements is a true statement.
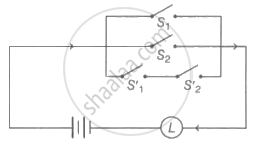
The symbolic form of the following circuit is (where p, q represents switches S1 and S2 closed respectively)
If c denotes the contradiction then the dual of the compound statement ∼p ∧ (q ∨ c) is ______
The negation of (p ∨ ∼q) ∧ q is ______
The Boolean expression ∼(q ⇒ ∼p) is equivalent to: ______
The Boolean expression ∼(p ∨ q) ∨ (∼p ∧ q) is equivalent to ______
The negation of the statement: "Getting above 95% marks is a necessary condition for Hema to get admission in good college'' is ______
Write the following statement in symbolic form.
4 is an odd number if 3 is not a prime factor of 6.
The statement ∼(p ↔ ∼q) is ______.
Write the negation of (p `leftrightarrow` q).
