Advertisements
Advertisements
Question
The negation of the statement (p ˄ q) `→` (r ˅ ∼ p) is ______.
Options
p ˄ q ˄ ∼ r
(p ˄ q) ˅ r
p ˅ q ˅ ∼ r
(p v q) ˄ (r ˅ s)
Solution
The negation of the statement (p ˄ q) `→` (r ˅ ∼ p) is p ˄ q ˄ ∼ r.
APPEARS IN
RELATED QUESTIONS
Examine whether each of the following statement patterns is a tautology or a contradiction or a contingency.
[~(~p ∧ ~q)] v q
Using truth table prove that ∼p ˄ q ≡ (p ˅ q) ˄ ∼p
Using truth table, prove that ~ p ∧ q ≡ (p ∨ q) ∧ ~ p
Write converse, inverse contrapositive of the statement "If two triangles are not congruent then their areas are not equal.
Write the following compound statement symbolically.
If Δ ABC is right-angled at B, then m∠A + m∠C = 90°
Write the following compound statement symbolically.
Hima Das wins gold medal if and only if she runs fast.
Construct the truth table of the following statement pattern.
(p ∧ q) ↔ (q ∨ r)
Construct the truth table of the following statement pattern.
p → [∼ (q ∧ r)]
Construct the truth table of the following statement pattern.
(q → p) ∨ (∼ p ↔ q)
Construct the truth table of the following statement pattern.
[p → (q → r)] ↔ [(p ∧ q) → r]
If p ∧ q is false and p ∨ q is true, then ______ is not true.
Construct the truth table of the following:
p → (q → p)
Construct the truth table of the following:
∼ (∼p ∧ ∼q) ∨ q
Construct the truth table of the following:
[(∼p ∨ q) ∧ (q → r)] → (p → r)
Express the following statement in symbolic form.
Mango is a fruit but potato is a vegetable.
Express the following statement in symbolic form.
Milk is white or grass is green.
Express the following statement in symbolic form.
I like playing but not singing.
Write the truth value of the following statement.
16 is an even number and 8 is a perfect square.
Write the negation of the following statement.
All men are animals.
Find the truth value of the following statement.
Neither 27 is a prime number nor divisible by 4.
Find the truth value of the following statement.
3 is a prime number and an odd number.
If p and q are true and r and s are false, find the truth value of the following compound statement.
p ∧ (q ∧ r)
If p and q are true and r and s are false, find the truth value of the following compound statement.
(p → q) ↔ ~(p ∨ q)
If p : He swims
q : Water is warm
Give the verbal statement for the following symbolic statement.
p ↔ ~ q
If p : He swims
q : Water is warm
Give the verbal statement for the following symbolic statement.
~ (p ∨ q)
Fill in the blanks :
Negation of “some men are animal” is –––––––––.
Assuming the first statement p and second as q. Write the following statement in symbolic form.
Kavita is brilliant and brave.
Assuming the first statement p and second as q. Write the following statement in symbolic form.
If Kiran drives the car, then Sameer will walk.
Assuming the first statement p and second as q. Write the following statement in symbolic form.
x3 + y3 = (x + y)3 if xy = 0.
Assuming the first statement p and second as q. Write the following statement in symbolic form.
The drug is effective though it has side effects.
Assuming the first statement p and second as q. Write the following statement in symbolic form.
If a real number is not rational, then it must be irrational.
Assuming the first statement p and second as q. Write the following statement in symbolic form.
It is not true that intelligent persons are neither polite nor helpful.
Assuming the first statement p and second as q. Write the following statement in symbolic form.
If the question paper is not easy then we shall not pass.
If p : Proof is lengthy.
q : It is interesting.
Express the following statement in symbolic form.
If proof is lengthy then it is interesting.
If p : Proof is lengthy.
q : It is interesting.
Express the following statement in symbolic form.
It is not true that the proof is lengthy but it is interesting.
Let p : Sachin wins the match.
q : Sachin is a member of Rajya Sabha.
r : Sachin is happy.
Write the verbal statement of the following.
∼ p ∨ q
Let p : Sachin wins the match.
q : Sachin is a member of Rajya Sabha.
r : Sachin is happy.
Write the verbal statement of the following.
p→(q ∨ r)
Let p : Sachin wins the match.
q : Sachin is a member of Rajya Sabha.
r : Sachin is happy.
Write the verbal statement of the following.
p → q
Let p : Sachin wins the match.
q : Sachin is a member of Rajya Sabha.
r : Sachin is happy.
Write the verbal statement of the following.
∼ (p ∨ q) ∧ r
Rewrite the following statement without using conditional –
(Hint : p → q ≡ ∼ p ∨ q)
If price increases, then demand falls.
Rewrite the following statement without using conditional –
(Hint : p → q ≡ ∼ p ∨ q)
If demand falls, then price does not increase.
Write the negation of the following.
Ramesh is intelligent and he is hard working.
Write the negation of the following.
An angle is a right angle if and only if it is of measure 90°.
Write the negation of the following.
Kanchanganga is in India and Everest is in Nepal.
Write the negation of the following.
If x ∈ A ∩ B, then x ∈ A and x ∈ B.
Rewrite the following statement without using the connective ‘If ... then’.
If a quadrilateral is rhombus then it is not a square.
Consider the following statements.
- If D is dog, then D is very good.
- If D is very good, then D is dog.
- If D is not very good, then D is not a dog.
- If D is not a dog, then D is not very good.
Identify the pairs of statements having the same meaning. Justify.
Write the negation of the following statement.
10 > 5 and 3 < 8
Write the negation of the following statement.
∀ n ∈ N, n + 3 > 9.
Without using truth table prove that:
~ (p ∨ q) ∨ (~ p ∧ q) ≡ ~ p
Write the following statements in symbolic form
Milk is white if and only if the sky is not blue
Write the following statements in symbolic form
If Kutab – Minar is in Delhi then Taj - Mahal is in Agra
Write the following statements in symbolic form
Even though it is not cloudy, it is still raining
Using truth table prove that p ˅ (q ˄ r) ≡ (p ˅ q) ˄ (p ˅ r)
Without using truth table show that -
(p ˅ q) ˄ (∼p v ∼q) ≡ (p ∧ ∼q) ˄ (∼p ∧ q)
Write the negation of p → q
If p : Every natural number is a real number.
q : Every integer is a complex number. Then truth values of p → q and p ↔ q are ______ and ______ respectively.
If (p ∧ ~ r) → (~ p ∨ q) is a false statement, then respective truth values of p, q and r are ______.
Given 'p' and 'q' as true and 'r' as false, the truth values of p v (q ∧ ~r) and (p → r) ∧ q are respectively
If p, q are true statement and r is false statement, then which of the following statements is a true statement.
The symbolic form of the following circuit is (where p, q represents switches S1 and S2 closed respectively)
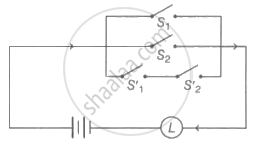
Which of the following is false?
If p and q are true and rands are false statements, then which of the following is true?
Let p : 7 is not greater than 4 and q : Paris is in France by two statements. Then ∼(p ∨ q) is the statement ______
The Boolean expression ∼(q ⇒ ∼p) is equivalent to: ______
The inverse of the statement "If its quality is good. then it is expensive.", is ______
The negation of ∼s ∨ (∼r ∧ s) is equivalent to ______
The statement, 'If I go to school, then I will get knowledge' is equivalent to ______
The Boolean expression ∼(p ∨ q) ∨ (∼p ∧ q) is equivalent to ______
The logical statement (∼p → q) ∧ (q → p) is equivalent to: ______
Let p, q and r be any three logical statements. Which of the following is true?
Write the following statement in symbolic form.
It is not true that `sqrt(2)` is a rational number.
The statement ∼(p ↔ ∼q) is ______.
Express the following compound statement symbolically:
Delhi is in India but Dhaka is not in Sri Lanka
Write the contrapositive of the inverse of the statement:
‘If two numbers are not equal, then their squares are not equal’.
From the following set of statements, select two statements which have similar meaning.
- If a man is judge, then he is honest.
- If a man is not a judge, then he is not honest.
- If a man is honest, then he is a judge.
- If a man is not honest, then he is not a judge.
If p, q are true statements and r, s are false statements, then write the truth value of the compound statement
(p `→` ∼ r) `→` (q ∧ s)
Write the negation of (p `leftrightarrow` q).
Construct the truth table for the statement pattern:
[(p → q) ∧ q] → p
