Advertisements
Advertisements
Question
Write the following statements in symbolic form
Even though it is not cloudy, it is still raining
Solution
Let p: It is cloudy.
q: It is still raining.
∴ The symbolic form of the given statement is ~p ∧ q
RELATED QUESTIONS
Examine whether each of the following statement patterns is a tautology or a contradiction or a contingency.
[~(~p ∧ ~q)] v q
Using truth table prove that p ↔ q = (p ∧ q) ∨ (~p ∧ ~q).
Using truth table, prove the following logical equivalence:
(p ∧ q) → r ≡ p → (q → r)
Using truth table prove that ∼p ˄ q ≡ (p ˅ q) ˄ ∼p
Using the truth table, prove the following logical equivalence :
p ↔ q ≡ (p ∧ q) ∨ (~p ∧ ~q)
Evaluate: ∫ x . log x dx
Write converse, inverse contrapositive of the statement "If two triangles are not congruent then their areas are not equal.
Write the following compound statement symbolically.
Angle is neither acute nor obtuse.
Write the following compound statement symbolically.
If Δ ABC is right-angled at B, then m∠A + m∠C = 90°
Write the following compound statement symbolically.
x is not irrational number but is a square of an integer.
Construct the truth table of the following statement pattern.
[(p → q) ∧ q] → p
Construct the truth table of the following statement pattern.
(p ∧ ∼q) ↔ (p → q)
Construct the truth table of the following statement pattern.
∼ p ∧ [(p ∨ ∼ q) ∧ q]
Construct the truth table of the following statement pattern.
(∼ p → ∼ q) ∧ (∼ q → ∼ p)
Construct the truth table of the following statement pattern.
[p → (q → r)] ↔ [(p ∧ q) → r]
If p ∧ q is false and p ∨ q is true, then ______ is not true.
Construct the truth table of the following:
p → (q → p)
Construct the truth table of the following:
∼ (∼p ∧ ∼q) ∨ q
Construct the truth table of the following:
[(p ∧ q) ∨ r] ∧ [∼r ∨ (p ∧ q)]
Determine the truth values of p and q in the following case:
(p ∨ q) is T and (p ∨ q) → q is F
Determine the truth values of p and q in the following case:
(p ∧ q) is F and (p ∧ q) → q is T
Express the following statement in symbolic form.
e is a vowel or 2 + 3 = 5
Express the following statement in symbolic form.
Mango is a fruit but potato is a vegetable.
Express the following statement in symbolic form.
Milk is white or grass is green.
Express the following statement in symbolic form.
I like playing but not singing.
Express the following statement in symbolic form.
Even though it is cloudy, it is still raining.
Write the truth value of the following statement.
Earth is a planet and Moon is a star.
Write the truth value of the following statement.
A quadratic equation has two distinct roots or 6 has three prime factors.
Write the negation of the following statement.
− 3 is a natural number.
Write the negation of the following statement.
2 + 3 ≠ 5
Write the truth value of the negation of the following statement.
`sqrt5` is an irrational number.
Write the truth value of the negation of the following statement.
London is in England.
Write the truth value of the negation of the following statement.
For every x ∈ N, x + 3 < 8.
Write the following statement in symbolic form.
If triangle is equilateral then it is equiangular.
Write the following statement in symbolic form.
It is not true that “i” is a real number.
Write the following statement in symbolic form.
Milk is white if and only if the sky is not blue.
Find the truth value of the following statement.
If a joint venture is a temporary partnership, then discount on purchase is credited to the supplier.
Find the truth value of the following statement.
Every accountant is free to apply his own accounting rules if and only if machinery is an asset.
Find the truth value of the following statement.
Neither 27 is a prime number nor divisible by 4.
If p and q are true and r and s are false, find the truth value of the following compound statement.
(p → q) ∨ (r ∧ s)
If p and q are true and r and s are false, find the truth value of the following compound statement.
~ [(~ p ∨ s) ∧ (~ q ∧ r)]
If p and q are true and r and s are false, find the truth value of the following compound statement.
(p → q) ↔ ~(p ∨ q)
If p and q are true and r and s are false, find the truth value of the following compound statement.
[(p ∨ s) → r] ∨ ~ [~ (p → q) ∨ s]
Assuming that the following statement is true,
p : Sunday is holiday,
q : Ram does not study on holiday,
find the truth values of the following statements.
If Sunday is not holiday then Ram studies on holiday.
Assuming that the following statement is true,
p : Sunday is holiday,
q : Ram does not study on holiday,
find the truth values of the following statements.
Sunday is a holiday and Ram studies on holiday.
If p : He swims
q : Water is warm
Give the verbal statement for the following symbolic statement.
p ↔ ~ q
If p : He swims
q : Water is warm
Give the verbal statement for the following symbolic statement.
~ (p ∨ q)
If p : He swims
q : Water is warm
Give the verbal statement for the following symbolic statement.
q ∧ ~ p
State whether the following statement is True or False:
The negation of 10 + 20 = 30 is, it is false that 10 + 20 ≠ 30.
Assuming the first statement p and second as q. Write the following statement in symbolic form.
The Sun has set and Moon has risen.
Assuming the first statement p and second as q. Write the following statement in symbolic form.
x3 + y3 = (x + y)3 if xy = 0.
Assuming the first statement p and second as q. Write the following statement in symbolic form.
If a real number is not rational, then it must be irrational.
Assuming the first statement p and second as q. Write the following statement in symbolic form.
It is not true that intelligent persons are neither polite nor helpful.
Assuming the first statement p and second as q. Write the following statement in symbolic form.
If the question paper is not easy then we shall not pass.
If p : Proof is lengthy.
q : It is interesting.
Express the following statement in symbolic form.
If proof is lengthy then it is interesting.
Let p : Sachin wins the match.
q : Sachin is a member of Rajya Sabha.
r : Sachin is happy.
Write the verbal statement of the following.
p → r
Let p : Sachin wins the match.
q : Sachin is a member of Rajya Sabha.
r : Sachin is happy.
Write the verbal statement of the following.
p → q
Rewrite the following statement without using conditional –
(Hint : p → q ≡ ∼ p ∨ q)
If price increases, then demand falls.
Write the negation of the following.
If ∆ABC is not equilateral, then it is not equiangular.
Write the negation of the following.
Kanchanganga is in India and Everest is in Nepal.
Write the negation of the following.
If x ∈ A ∩ B, then x ∈ A and x ∈ B.
Assuming the following statement.
p : Stock prices are high.
q : Stocks are rising.
to be true, find the truth value of the following.
Stock prices are high or stocks are not rising iff stocks are rising.
Rewrite the following statement without using the connective ‘If ... then’.
If a quadrilateral is rhombus then it is not a square.
Consider the following statements.
- If D is dog, then D is very good.
- If D is very good, then D is dog.
- If D is not very good, then D is not a dog.
- If D is not a dog, then D is not very good.
Identify the pairs of statements having the same meaning. Justify.
Write the negation of the following statement.
I will have tea or coffee.
Write the negation of the following statement.
∀ n ∈ N, n + 3 > 9.
Negation of p → (p ˅ ∼ q) is ______
The negation of the statement (p ˄ q) `→` (r ˅ ∼ p) is ______.
Find the negation of 10 + 20 = 30
Write the following compound statements symbolically.
Triangle is equilateral or isosceles
Without using truth table prove that:
~ (p ∨ q) ∨ (~ p ∧ q) ≡ ~ p
Write the negation of the statement “An angle is a right angle if and only if it is of measure 90°”
Using truth table prove that p ˅ (q ˄ r) ≡ (p ˅ q) ˄ (p ˅ r)
Choose the correct alternative:
Negation of p → (p ˅ ~q) is
Choose the correct alternative:
A biconditional statement is the conjunction of two ______ statements
Write the negation of the statement “An angle is a right angle if and only if it is of measure 90°”
If p : Every natural number is a real number.
q : Every integer is a complex number. Then truth values of p → q and p ↔ q are ______ and ______ respectively.
If (p ∧ ~ r) → (~ p ∨ q) is a false statement, then respective truth values of p, q and r are ______.
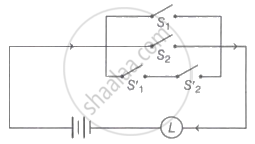
The symbolic form of the following circuit is (where p, q represents switches S1 and S2 closed respectively)
If q: There are clouds in the sky then p: it is raining. The symbolic form is ______
If c denotes the contradiction then the dual of the compound statement ∼p ∧ (q ∨ c) is ______
Which of the following is false?
If p and q are true and rands are false statements, then which of the following is true?
Let p : 7 is not greater than 4 and q : Paris is in France by two statements. Then ∼(p ∨ q) is the statement ______
Which of the following is NOT true for p → q.
The inverse of the statement "If its quality is good. then it is expensive.", is ______
The negation of ∼s ∨ (∼r ∧ s) is equivalent to ______
The statement, 'If I go to school, then I will get knowledge' is equivalent to ______
The negation of the statement: "Getting above 95% marks is a necessary condition for Hema to get admission in good college'' is ______
Write the converse, inverse, and contrapositive of the statement. "If 2 + 5 = 10, then 4 + 10 = 20."
Let p, q and r be any three logical statements. Which of the following is true?
Which of the following is logically equivalent to `∼(∼p \implies q)`?
Converse of the statement q `rightarrow` p is ______.
Write the following statement in symbolic form.
It is not true that `sqrt(2)` is a rational number.
Express the following compound statement symbolically:
3 + 8 ≥ 12 if and only if 5 × 4 ≤ 25
Write the contrapositive of the inverse of the statement:
‘If two numbers are not equal, then their squares are not equal’.
If p, q are true statements and r, s are false statements, then write the truth value of the compound statement
(p `→` ∼ r) `→` (q ∧ s)
Using the statements
p: Seema is fat,
q: Seema is happy,
Write the following statements in symbolic form;
- Seema is thin and happy.
- If Seema is fat then she is unhappy.
Construct the truth table for the statement pattern:
[(p → q) ∧ q] → p
