Advertisements
Advertisements
Question
Find the acceleration of the block of mass M in the situation of figure in the following. The coefficient of friction between the two blocks is μ1 and that between the bigger block and the ground is μ2.
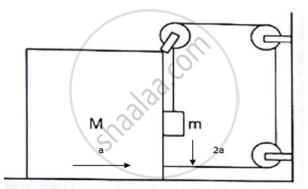
Solution
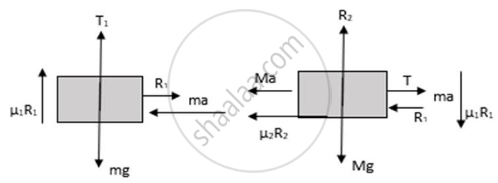
Let the acceleration of block of mass M is ‘a’ towards right. So, the block ‘m’ must go down with an acceleration ‘2a’.
As the block ‘m’ is in contact with the block ‘M’, it will also have acceleration ‘a’ towards right. So, it will experience two inertial forces as shown in figure (b). From free body diagram
R1 – ma = 0
⇒ R1 = ma (i)
Also,
2ma + T – Mg + μ1R1 = 0
⇒ T = Mg – (2 + μ1) ma (ii)
Using the free body diagram (c), we can write,
T + μ1R1 + Mg – R2 = 0
Substituting the value of R1 from (i), we get,
R2 = T + μ1 ma + mg
Substituting the value of T from (ii), we get,
R2 = (Mg – 2ma – μ1ma) = μ1 ma + Mg + ma
∴ R2 = Mg + Ma – 2ma ….(iii)
Again, using the free body diagrams (c),
T + T – R – Ma – μ2R2 = 0
⇒ 2T – Ma – ma – μ2(Mg + mg – 2ma) = 0
Substituting the values of R1 and R2 from (i) and (iii), we get:
2T = (M + m)a + μ2 (Mg + mg – 2ma) ….(iv)
From equations (ii) and (iv), we have:
2T = 2mg – 2(2 + μ1) ma
= (M + m) a + μ1(Mg + mg – 2ma)
⇒ 2mg – μ2 (M + m)g = a[M + m – 2μ2m + 4m + 2μ1m]
Therefore, the acceleration of the block of mass M in the given situation is given by `a = (2m + μ2(M + m)g)/(M + m(5 + 2(μ1 - μ2))`
APPEARS IN
RELATED QUESTIONS
A body of mass M is kept on a rough horizontal surface (friction coefficient = μ). A person is trying to pull the body by applying a horizontal force but the body is not moving. The force by the surface on A is F, where
A block A kept on an inclined surface just begins to slide if the inclination is 30°. The block is replaced by another block B and it is found that it just begins to slide if the inclination is 40°.
A boy of mass M is applying a horizontal force to slide a box of mass M' on a rough horizontal surface. The coefficient of friction between the shoes of the boy and the floor is μ and that between the box and the floor is μ'. In which of the following cases it is certainly not possible to slide the box?
The contact force exerted by a body A on another body B is equal to the normal force between the bodies We conclude that
(a) the surface must be frictionless
(b) the force of friction between the bodies is zero
(c) the magnitude of normal force equal that of friction
(d) the bodies may be rough but they don't slip on each other.
A block is placed on a rough floor and a horizontal force F is applied on it. The force of friction f by the floor on the block is measured for different values of F and a graph is plotted between them.
(a) The graph is a straight line of slope 45°.
(b) The graph is a straight line parallel to the F-axis.
(c) The graph is a straight line of slope 45° for small F and a straight line parallel to the F-axis for large F.
(d) There is a small kink on the graph.
A block slides down an inclined surface of inclination 30° with the horizontal. Starting from rest it covers 8 m in the first two seconds. Find the coefficient of kinetic friction between the two.
A body of mass 2 kg is lying on a rough inclined plane of inclination 30°. Find the magnitude of the force parallel to the incline needed to make the block move (a) up the incline (b) down the incline. Coefficient of static friction = 0.2.
A body starts slipping down an incline and moves half metre in half second. How long will it take to move the next half metre?
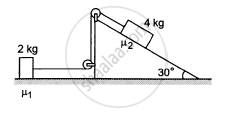
If the tension in the string in the following figure is 16 N and the acceleration of each block is 0.5 m/s2, find the friction coefficients at the two contact with the blocks.
The friction coefficient between an athelete's shoes and the ground is 0.90. Suppose a superman wears these shoes and races for 50 m. There is no upper limit on his capacity of running at high speeds. (a) Find the minimum time that he will have to take in completing the 50 m starting from rest. (b) Suppose he takes exactly this minimum time to complete the 50 m, what minimum time will he take to stop?
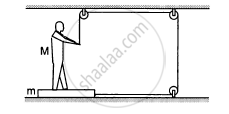
The friction coefficient between the board and the floor shown in the following figure is μ. Find the maximum force that the man can exert on the rope so that the board does not slip on the floor.
A 2 kg block is placed over a 4 kg block and both are placed on a smooth horizontal surface. The coefficient of friction between the block is 0.20. Find the acceleration of the two blocks if a horizontal force of 12 N is applied to (a) the upper block, (b) the lower block. Take g = 10 m/s2.
Consider the situation shown in the following figure. Suppose a small electric field E exists in the space in the vertically charge Q on its top surface. The friction coefficient between the two blocks is μ but the floor is smooth. What maximum horizontal force F can be applied without disturbing the equilibrium?
[Hint: The force on a charge Q bye the electric field E is F = QE in the direction of E.]
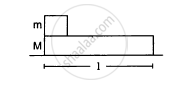
In the following figure shows a small block of mass m kept at the left end of a larger block of mass M and length l. The system can slide on a horizontal road. The system is started towards right with an initial velocity v. The friction coefficient between the road and the bigger block is μ and that between the block is μ/2. Find the time elapsed before the smaller blocks separates from the bigger block.
An inclined plane is bent in such a way that the vertical cross-section is given by Y = `x^2/4` where y is in vertical and x in horizontal direction. If the upper surface of this curved plane is rough with coefficient of friction µ = 0.5, the maximum height in cm at which a stationary block will not slip downward is ______ cm.
