Advertisements
Advertisements
Question
A body of mass 2 kg is lying on a rough inclined plane of inclination 30°. Find the magnitude of the force parallel to the incline needed to make the block move (a) up the incline (b) down the incline. Coefficient of static friction = 0.2.
Solution
(a) To make the block move up the incline, the applied force should be equal and opposite to the net force acting down the incline.
Applied force = μR + 2g sin 30° (1)
(where μ is the coefficient of static friction)
R = mg cos 30°
Substituting the respective values in Equation (1), we get
`=0.2xx(9.8)sqrt3+2xx9.8xx(1/2)`
3.39 + 9.8 ≈ 13 N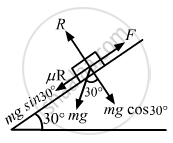
With this minimum force, the body moves up the incline with a constant velocity as the net force on it is zero.
(b) Net force acting down the incline is given by
F = 2g sin 30° − μR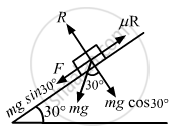
`=2xx9.8xx1/2-3.99`
= 6.41 N
Because F = 6.41 N, the body will move down the incline with acceleration, hence the force required is zero.
APPEARS IN
RELATED QUESTIONS
In a situation the contact force by a rough horizontal surface on a body placed on it has constant magnitude. If the angle between this force and the vertical is decreased, the frictional force between the surface and the body will
A boy of mass M is applying a horizontal force to slide a box of mass M' on a rough horizontal surface. The coefficient of friction between the shoes of the boy and the floor is μ and that between the box and the floor is μ'. In which of the following cases it is certainly not possible to slide the box?
A body slipping on a rough horizontal plane moves with a deceleration of 4.0 m/s2. What is the coefficient of kinetic friction between the block and the plane?
A block is projected along a rough horizontal road with a speed of 10 m/s. If the coefficient of kinetic friction is 0.10, how far will it travel before coming to rest?
A block of mass m is kept on a horizontal table. If the static friction coefficient is μ, find the frictional force acting on the block.
Suppose the block of the previous problem is pushed down the incline with a force of 4 N. How far will the block move in the first two seconds after starting from rest? The mass of the block is 4 kg.
The angle between the resultant contact force and the normal force exerted by a body on the other is called the angle of friction. Show that, if λ be the angle of friction and μ the coefficient of static friction λ ≤ tan−1 μ.
Consider the situation shown in the following figure. Calculate (a) the acceleration of the 1.0 kg blocks, (b) the tension in the string connecting the 1.0 kg blocks and (c) the tension in the string attached to 0.50 kg.
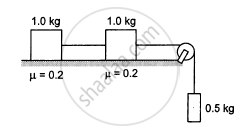
If the tension in the string in the following figure is 16 N and the acceleration of each block is 0.5 m/s2, find the friction coefficients at the two contact with the blocks.
The friction coefficient between a road and the type of a vehicle is 4/3. Find the maximum incline the road may have so that once had brakes are applied and the wheel starts skidding, the vehicle going down at a speed of 36 km/hr is stopped within 5 m.
A block of mass M is kept on a rough horizontal surface. The coefficient of static friction between the block and the surface is μ. The block is to be pulled by applying a force to it. What minimum force is needed to slide the block? In which direction should this force act?
The friction coefficient between the board and the floor shown in the following figure is μ. Find the maximum force that the man can exert on the rope so that the board does not slip on the floor.
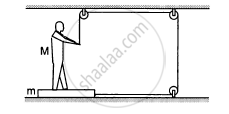
Suppose the entire system of the previous questions is kept inside an elevator which is coming down with an acceleration a < g. Repeat parts (a) and (b).
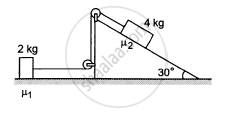
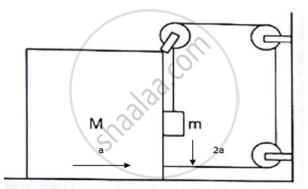
Find the acceleration of the block of mass M in the situation of figure in the following. The coefficient of friction between the two blocks is μ1 and that between the bigger block and the ground is μ2.
A block of mass 2 kg is pushed against a rough vertical wall with a force of 40 N, coefficient of static friction being 0.5. Another horizontal force of 15 N, is applied on the block in a direction parallel to the wall. Will the block move? If yes, in which direction? If no, find the frictional force exerted by the wall on the block.
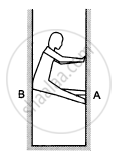
A person (40 kg) is managing to be at rest between two vertical walls by pressing one wall A by his hands and feet and the other wall B by his back (in the following figure). Assume that the friction coefficient between his body and the walls is 0.8 and that limiting friction acts at all the contacts. (a) Show that the person pushes the two wall with equal force. (b) Find the normal force exerted by either wall on the person. Take g = 10 m/s2.
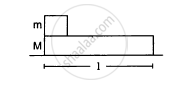
In the following figure shows a small block of mass m kept at the left end of a larger block of mass M and length l. The system can slide on a horizontal road. The system is started towards right with an initial velocity v. The friction coefficient between the road and the bigger block is μ and that between the block is μ/2. Find the time elapsed before the smaller blocks separates from the bigger block.
A block placed on a rough horizontal surface is pulled by a horizontal force F. Let f be the force applied by the rough surface on the block. Plot a graph of f versus F.
