Advertisements
Advertisements
प्रश्न
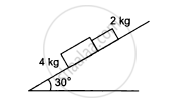
A body of mass 2 kg is lying on a rough inclined plane of inclination 30°. Find the magnitude of the force parallel to the incline needed to make the block move (a) up the incline (b) down the incline. Coefficient of static friction = 0.2.
उत्तर
(a) To make the block move up the incline, the applied force should be equal and opposite to the net force acting down the incline.
Applied force = μR + 2g sin 30° (1)
(where μ is the coefficient of static friction)
R = mg cos 30°
Substituting the respective values in Equation (1), we get
`=0.2xx(9.8)sqrt3+2xx9.8xx(1/2)`
3.39 + 9.8 ≈ 13 N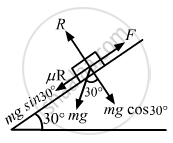
With this minimum force, the body moves up the incline with a constant velocity as the net force on it is zero.
(b) Net force acting down the incline is given by
F = 2g sin 30° − μR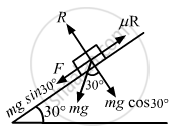
`=2xx9.8xx1/2-3.99`
= 6.41 N
Because F = 6.41 N, the body will move down the incline with acceleration, hence the force required is zero.
APPEARS IN
संबंधित प्रश्न
In a situation the contact force by a rough horizontal surface on a body placed on it has constant magnitude. If the angle between this force and the vertical is decreased, the frictional force between the surface and the body will
A boy of mass M is applying a horizontal force to slide a box of mass M' on a rough horizontal surface. The coefficient of friction between the shoes of the boy and the floor is μ and that between the box and the floor is μ'. In which of the following cases it is certainly not possible to slide the box?
The contact force exerted by a body A on another body B is equal to the normal force between the bodies We conclude that
(a) the surface must be frictionless
(b) the force of friction between the bodies is zero
(c) the magnitude of normal force equal that of friction
(d) the bodies may be rough but they don't slip on each other.
A block is placed on a rough floor and a horizontal force F is applied on it. The force of friction f by the floor on the block is measured for different values of F and a graph is plotted between them.
(a) The graph is a straight line of slope 45°.
(b) The graph is a straight line parallel to the F-axis.
(c) The graph is a straight line of slope 45° for small F and a straight line parallel to the F-axis for large F.
(d) There is a small kink on the graph.
A body slipping on a rough horizontal plane moves with a deceleration of 4.0 m/s2. What is the coefficient of kinetic friction between the block and the plane?
A block slides down an inclined surface of inclination 30° with the horizontal. Starting from rest it covers 8 m in the first two seconds. Find the coefficient of kinetic friction between the two.
Repeat part (a) of problem 6 if the push is applied horizontally and not parallel to the incline.
In a children-park an inclined plane is constructed with an angle of incline 45° in the middle part (in the following figure). Find the acceleration of boy sliding on it if the friction coefficient between the cloth of the boy and the incline is 0.6 and g = 19 m/s2.

Consider the situation shown in the following figure. Calculate (a) the acceleration of the 1.0 kg blocks, (b) the tension in the string connecting the 1.0 kg blocks and (c) the tension in the string attached to 0.50 kg.
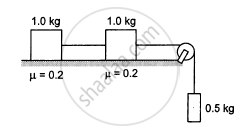
If the tension in the string in the following figure is 16 N and the acceleration of each block is 0.5 m/s2, find the friction coefficients at the two contact with the blocks.
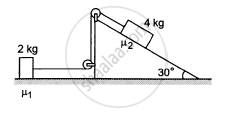
The friction coefficient between a road and the type of a vehicle is 4/3. Find the maximum incline the road may have so that once had brakes are applied and the wheel starts skidding, the vehicle going down at a speed of 36 km/hr is stopped within 5 m.
In the following figure shows two blocks in contact sliding down an inclined surface of inclination 30°. The friction coefficient between the block of mass 2.0 kg and the incline is μ1, and that between the block of mass 4.0 kg and incline is μ2. Calculate the acceleration of the 2.0 kg block if (a) μ1 = 0.20 and μ2 = 0.30, (b) μ1 = 0.30 and μ2 = 0.20. Take g = 10 m/s2.
The friction coefficient between the board and the floor shown in the following figure is μ. Find the maximum force that the man can exert on the rope so that the board does not slip on the floor.
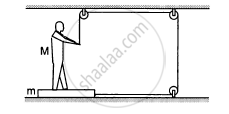
Suppose the entire system of the previous questions is kept inside an elevator which is coming down with an acceleration a < g. Repeat parts (a) and (b).
Consider the situation shown in the following figure. Suppose a small electric field E exists in the space in the vertically charge Q on its top surface. The friction coefficient between the two blocks is μ but the floor is smooth. What maximum horizontal force F can be applied without disturbing the equilibrium?
[Hint: The force on a charge Q bye the electric field E is F = QE in the direction of E.]
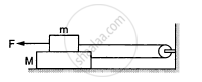
A block of mass m slips on a rough horizontal table under the action of a horizontal force applied to it. The coefficient of friction between the block and the table is μ. The table does not move on the floor. Find the total frictional force applied by the floor on the legs of the table. Do you need the friction coefficient between the table and the floor or the mass of the table?
A block of mass 2 kg is pushed against a rough vertical wall with a force of 40 N, coefficient of static friction being 0.5. Another horizontal force of 15 N, is applied on the block in a direction parallel to the wall. Will the block move? If yes, in which direction? If no, find the frictional force exerted by the wall on the block.
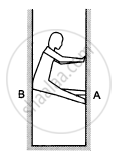
A person (40 kg) is managing to be at rest between two vertical walls by pressing one wall A by his hands and feet and the other wall B by his back (in the following figure). Assume that the friction coefficient between his body and the walls is 0.8 and that limiting friction acts at all the contacts. (a) Show that the person pushes the two wall with equal force. (b) Find the normal force exerted by either wall on the person. Take g = 10 m/s2.
An inclined plane is bent in such a way that the vertical cross-section is given by Y = `x^2/4` where y is in vertical and x in horizontal direction. If the upper surface of this curved plane is rough with coefficient of friction µ = 0.5, the maximum height in cm at which a stationary block will not slip downward is ______ cm.
