Advertisements
Advertisements
Question
Find all trigonometric functions of angle in standard position whose terminal arm passes through point (3, −4).
Solution
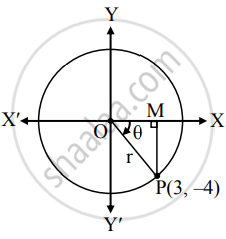
Let θ be the measure of the angle in standard position whose terminal arm passes through P(3, – 4).
∴ x = 3 and y = - 4
r = OP
∴ r = `sqrt((3 - 0)^2 + (- 4 - 0)^2)`
= `sqrt(9 + 16)`
= 5
∴ sin θ = `y/"r" = - 4/5`
cos θ = `x/"r" = 3/5`
tan θ = `y/x = (-4)/3 = -4/3`
cosec θ = `"r"/y = 5/(-4) = -5/4`
sec θ = `"r"/x = 5/3`
cot θ = `x/y = 3/(-4) = -3/4`
Notes
APPEARS IN
RELATED QUESTIONS
Find the trigonometric function of :
0°
Find the trigonometric function of :
30°
Find the trigonometric functions of :
180°
Find the trigonometric function of :
210°
Find the trigonometric functions of :
330°
Find the trigonometric functions of :
−45°
Find the trigonometric functions of :
−60°
Find the trigonometric functions of :
− 90°
Find the trigonometric functions of :
−120°
Find the trigonometric functions of :
−225°
Find the trigonometric functions of :
−240°
Find the trigonometric functions of :
−270°
Select the correct option from the given alternatives:
The value of the expression cos1°. cos2°. cos3° … cos179° =
Select the correct option from the given alternatives:
If α is a root of 25cos2θ + 5cosθ – 12 = 0, `pi/2` < α < π, then sin2α is equal to
Select the correct option from the given alternatives:
The cotangent of the angles `pi/3, pi/4 and pi/6` are in
Find the trigonometric functions of 225°.
Answer the following:
Find the trigonometric functions of :
270°
Answer the following:
Find the trigonometric functions of :
315°
Answer the following:
Find the trigonometric functions of :
−150°
Answer the following:
Find the trigonometric functions of :
−180°
Answer the following:
Find the trigonometric functions of :
−300°
Answer the following:
Find the trigonometric functions of :
−330°
Find the trigonometric functions of 120°.
