Advertisements
Advertisements
Question
Find all the zeroes of `(x^4 + x^3 – 23x^2 – 3x + 60)`, if it is given that two of its zeroes are `sqrt3 and –sqrt3`.
Advertisements
Solution
Let f(x) =`x^4 + x^3 – 23x^2 – 3x + 60`
Since `sqrt3` and `–sqrt3` are the zeroes of f(x), it follows that each one of (x – √3) and (x + √3) is a factor of f(x).
Consequently, `(x – sqrt3) (x + sqrt3) = (x^2 – 3)`is a factor of f(x).
On dividing f(x) by `(x^2 – 3)`, we get:
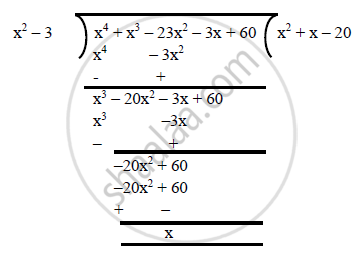
f(x) = 0
⇒ `(x^2 + x – 20) (x^2 – 3) = 0`
⇒ `(x^2 + 5x – 4x – 20) (x^2 – 3)`
⇒ `[x(x + 5) – 4(x + 5)] (x^2 – 3)`
⇒ `(x – 4) (x + 5) (x – sqrt3) (x + sqrt3) = 0`
⇒ `x = 4 or x = -5 or x = sqrt3 or x = -sqrt3`
Hence, all the zeroes are √3, -√3, 4 and -5.
APPEARS IN
RELATED QUESTIONS
Find the zeroes of the following quadratic polynomial and verify the relationship between the zeroes and the coefficients:
t2 – 15
Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients
`q(x)=sqrt3x^2+10x+7sqrt3`
If α and β are the zeros of the quadratic polynomial f(x) = ax2 + bx + c, then evaluate α2β + αβ2
If a and are the zeros of the quadratic polynomial f(x) = 𝑥2 − 𝑥 − 4, find the value of `1/alpha+1/beta-alphabeta`
Find a cubic polynomial with the sum, sum of the product of its zeroes taken two at a time, and product of its zeros as 3, −1 and −3 respectively.
Find the zeroes of the polynomial f(x) = `2sqrt3x^2-5x+sqrt3` and verify the relation between its zeroes and coefficients.
Find the zeroes of the quadratic polynomial `2x^2 ˗ 11x + 15` and verify the relation between the zeroes and the coefficients.
If (x+a) is a factor of the polynomial `2x^2 + 2ax + 5x + 10`, find the value of a.
If 3 and –3 are two zeroes of the polynomial `(x^4 + x^3 – 11x^2 – 9x + 18)`, find all the zeroes of the given polynomial.
If α, β, γ are are the zeros of the polynomial f(x) = x3 − px2 + qx − r, the\[\frac{1}{\alpha\beta} + \frac{1}{\beta\gamma} + \frac{1}{\gamma\alpha} =\]
If two of the zeros of the cubic polynomial ax3 + bx2 + cx + d are each equal to zero, then the third zero is
If two zeros x3 + x2 − 5x − 5 are \[\sqrt{5}\ \text{and} - \sqrt{5}\], then its third zero is
If 2 and `1/2` are the zeros of px2 + 5x + r, then ______.
For the following, find a quadratic polynomial whose sum and product respectively of the zeroes are as given. Also find the zeroes of these polynomials by factorisation.
`(-3)/(2sqrt(5)), -1/2`
The only value of k for which the quadratic polynomial kx2 + x + k has equal zeros is `1/2`
Find the zeroes of the following polynomials by factorisation method and verify the relations between the zeroes and the coefficients of the polynomials:
`7y^2 - 11/3 y - 2/3`
If the zeroes of the polynomial x2 + px + q are double in value to the zeroes of the polynomial 2x2 – 5x – 3, then find the values of p and q.
If one zero of the polynomial p(x) = 6x2 + 37x – (k – 2) is reciprocal of the other, then find the value of k.
Find the sum and product of the roots of the quadratic equation 2x2 – 9x + 4 = 0.
If α, β are zeroes of the quadratic polynomial x2 – 5x + 6, form another quadratic polynomial whose zeroes are `1/α, 1/β`.
