Advertisements
Advertisements
प्रश्न
Find all the zeroes of `(x^4 + x^3 – 23x^2 – 3x + 60)`, if it is given that two of its zeroes are `sqrt3 and –sqrt3`.
उत्तर
Let f(x) =`x^4 + x^3 – 23x^2 – 3x + 60`
Since `sqrt3` and `–sqrt3` are the zeroes of f(x), it follows that each one of (x – √3) and (x + √3) is a factor of f(x).
Consequently, `(x – sqrt3) (x + sqrt3) = (x^2 – 3)`is a factor of f(x).
On dividing f(x) by `(x^2 – 3)`, we get:
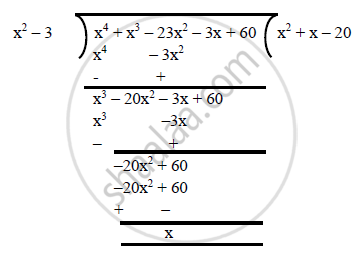
f(x) = 0
⇒ `(x^2 + x – 20) (x^2 – 3) = 0`
⇒ `(x^2 + 5x – 4x – 20) (x^2 – 3)`
⇒ `[x(x + 5) – 4(x + 5)] (x^2 – 3)`
⇒ `(x – 4) (x + 5) (x – sqrt3) (x + sqrt3) = 0`
⇒ `x = 4 or x = -5 or x = sqrt3 or x = -sqrt3`
Hence, all the zeroes are √3, -√3, 4 and -5.
APPEARS IN
संबंधित प्रश्न
Find the zeroes of the following quadratic polynomial and verify the relationship between the zeroes and the coefficients.
4u2 + 8u
If α and β are the zeros of the quadratic polynomial f(x) = ax2 + bx + c, then evaluate `beta/(aalpha+b)+alpha/(abeta+b)`
If α and β are the zeros of the quadratic polynomial f(x) = ax2 + bx + c, then evaluate :
`a(α^2/β+β^2/α)+b(α/β+β/α)`
If α and β are the zeros of the quadratic polynomial p(y) = 5y2 − 7y + 1, find the value of `1/alpha+1/beta`
If the sum of the zeros of the quadratic polynomial f(t) = kt2 + 2t + 3k is equal to their product, find the value of k.
If α and β are the zeros of a quadratic polynomial such that α + β = 24 and α − β = 8, find a quadratic polynomial having α and β as its zeros.
Find the zeroes of the polynomial f(x) = `2sqrt3x^2-5x+sqrt3` and verify the relation between its zeroes and coefficients.
If one of the zeroes of a quadratic polynomial of the form x2 + ax + b is the negative of the other, then it ______.
The only value of k for which the quadratic polynomial kx2 + x + k has equal zeros is `1/2`
Find the zeroes of the polynomial x2 + 4x – 12.
