Find the area of quadrilateral whose vertices are A(−3, 1), B(−2, −2), C(3, -1), D(1, 4) - Mathematics and Statistics

Find the area of quadrilateral whose vertices are

A(−3, 1), B(−2, −2), C(3, -1), D(1, 4)

Sum

A(−3, 1), B(−2, −2), C(3, -1), D(1, 4)

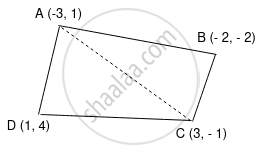
A(`square`ABCD) = A(ΔABC) + A(ΔACD)

Area of a triangle = `1/2|("x"_1,"y"_1,1),("x"_2,"y"_2,1),("x"_3,"y"_3,1)|`

A(ΔABC) = `1/2|(-3, 1, 1),(-2, -2, 1),(3, -1, 1)|`

= `1/2[-3(-2 - (- 1)) - 1(-2 - 3) + 1(2 - (- 6))]`

= `1/2[-3(-2 + 1) - 1(-2 - 3) + 1(2 + 6)]`

= `1/2[-3(-1)-1(-5)+1(8)]`

= `1/2 ( 3 + 5 + 8)`

= `1/2(16)`

∴ A(ΔABC) = 8 sq. units

A(ΔACD) = `1/2|(-3, 1, 1),(3, -1, 1),(1, 4, 1)|`

= `1/2[-3(-1-4)-1(3-1)+1(12 - (- 1))]`

= `1/2[-3(-5)-1(2)+1(13)]`

= `1/2(15-2+13)`

= `1/2(26)`

∴ A(ΔACD) = 13 sq. units

∴ A(`square`ABCD) = A(ΔABC) + A(ΔACD)

= 8 + 13

= 21 sq. units

shaalaa.com

Application of Determinants - Area of Triangle and Collinearity of Three Points

Is there an error in this question or solution?

Chapter 4: Determinants and Matrices - Exercise 4.3 [Page 75]

Chapter 4 Determinants and Matrices
Exercise 4.3 | Q 6 | Page 75

Find the area of triangle whose vertices are

A(5, 8), B(5, 0) C(1, 0)

Find the area of triangle whose vertices are

`"P"(3/2, 1), "Q"(4, 2), "R"(4, (-1)/2)`

Find the area of triangle whose vertices are

M(0, 5), N(−2, 3), T(1, −4)

Find the value of k, if the area of triangle whose vertices are P(k, 0), Q(2, 2), R(4, 3) is `3/2 "sq.unit"`

Examine the collinearity of the following set of point:

A(3, −1), B(0, −3), C(12, 5)

Examine the collinearity of the following set of point:

P(3, −5), Q(6, 1), R(4, 2)

Examine the collinearity of the following set of point:

`"L"(0, 1/2), "M"(2, -1), "N"(-4, 7/2)`

Select the correct option from the given alternatives:

If A(0,0), B(1,3) and C(k,0) are vertices of triangle ABC whose area is 3 sq.units then value of k is