Advertisements
Advertisements
Question
Find the equation of the circle which touches the both axes in first quadrant and whose radius is a.
Sum
Solution
Clearly centre of the circle = (a, a) and radius = a
Equation of circle with radius r and centre (h, k) is (x – h)2 + (y – k)2 = r2
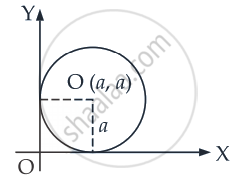
So, the equation of the required circle
⇒ (x – a)2 + (y – a)2 = a2
⇒ x2 – 2ax + a2 + y2 – 2ay + a2 = a2
⇒ x2 + y2 – 2ax – 2ay + a2 = 0
Hence, the required equation is x2 + y2 – 2ax – 2ay + a2 = 0
shaalaa.com
Is there an error in this question or solution?
