Advertisements
Advertisements
Question
Find the least number that must be subtracted to 6666 so that it becomes a perfect square. Also, find the square root of the perfect square thus obtained
Solution
Let us work out the process of finding the square root of 6666 by long division method.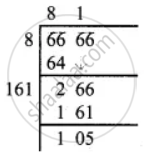
The remainder in the last step is 105.
Is if 105 be subtracted from the given number the remainder will be zero and the new number will be a perfect square.
∴ The required number is 105.
The square number is 6666 – 105 = 6561
APPEARS IN
RELATED QUESTIONS
Find the number of digits in the square root of the following numbers (without any calculation).
4489
Find the least number which must be added to the following number so as to get a perfect square. Also find the square root of the perfect square so obtained.
1825
Find the length of the side of a square whose area is 441 m2.
Find the square of the following number using the identity (a − b)2 = a2 − 2ab + b2:
999
Find the square of the following number by visual method:
95
Find the square root the following by long division method:
1745041
Find the least number which must be subtracted from the following numbers to make them a perfect square:
16160
Find the square root of: `(1764)/(2809)`
What is the least number that should be added to 6200 to make it a perfect square?
A General wishes to draw up his 7500 soldiers in the form of a square. After arranging, he found out that some of them are left out. How many soldiers were left out?
