Advertisements
Advertisements
Question
Find the radius of gyration of a uniform disc about an axis perpendicular to its plane and passing through its center.
Solution
M.I. of a uniform disc about an axis perpendicular to the plane and passing through its centre: I = `"MR"^2/2`
Since I = MK2
`"MR"^2/2`= MK2
`"MR"^2/(2"M")` = K2
K = `sqrt(("MR"^2)/(2"M")) = "R"/sqrt2`
APPEARS IN
RELATED QUESTIONS
Define radius of gyration
Answer in brief:
Why is it useful to define the radius of gyration?
Discuss the necessity of radius of gyration.
A cyclist riding a bicycle at a speed of `14sqrt3` m/s takes a turn around a circular road of radius `20sqrt3` m without skidding. Given g = 9.8 m/s2, what is his inclination to the vertical ______.
The ratio of radii of gyration of a ring to a disc (both circular) of same radii and mass, about a tangential axis perpendicular to the plane is
The radius of the earth and the radius of orbit around the sun are 6371 km and 149 x 106 km respectively. The order of magnitude of the diameter of the orbit is greater than that of earth by ______.
The radius of gyration of a homogeneous body is independent of ______.
The radius of gyration of a uniform rod of length `l`, about an axis passing through a point `l/4` away from the centre of the rod, and perpendicular to it, is: ____________.
Four particles each of mass 'M' are placed at corners of a square of side 'L'. The radius of gyration of the system about an axis perpendicular to the square and passing through its centre is ______.
A flywheel of mass 2 kg has radius of gyration 0.5m. If it makes 10 r.p.s. then its rotational kinetic energy will be ______.
A fly wheel is accelerated uniformly from rest and rotates through 5 rad in the first second. The angle rotated by the fly wheel in the next second, will be ______.
A circular disc of radius R is removed from a bigger circular disc of radius 2R such that the circumferences of the discs coincide. The centre of mass of the new disc is α/R form the centre of the bigger disc. The value of α is ______.
Let M be the mass and L be the length of a thin uniform rod. In first case, axis of rotation is passing through centre and perpendicular to the length of the rod. In second case, axis of rotation is passing through one end and perpendicular to the length of the rod. The ratio of radius of gyration in first case to second case is ______.
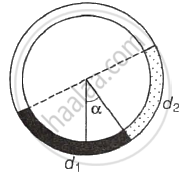
There is a circular tube in a vertical plane. Two liquids which do not mix and of densities d1 and d2 are filled in the tube. Each liquid subtends 90° angle at centre. Radius joining their interface makes an angle α with vertical. Ratio d1/d2 is ______.
What is the radius of gyration of a right circular cone of base radius R for rotation about the central symmetry axis of the cone?
Define radius of gyration
On what factors does radius of gyration depend?
On what factors radius of gyration does not depend?
Can you locate some similarity between the centre of mass and radius of gyration?
What can you infer if a uniform ring and a uniform disc have the same radius of gyration?
Define the Necessity radius of gyration.
