Advertisements
Advertisements
Question
Find the sum of odd natural numbers from 1 to 101
Solution
The odd natural numbers from 1 to 101 are
1, 3, 5, ....., 101
The above sequence is an A.P.
∴ a = 1, d = 3 – 1 = 2
Let the number of terms in the A.P. be n.
Then, tn = 101
Since tn = a + (n – 1)d,
101 = 1 + (n – 1)(2)
∴ 101 = 1 + 2n – 2
∴ 101 = 2n – 1
∴ 102 = 2n
∴ n = `102/2` = 51
Now, Sn = `"n"/2 ("t"_1 + "t"_"n")`
∴ S51 = `51/2 (1 + 101)`
= `51/2 (102)`
= 51 × 51
= 2601
∴ The sum of odd natural numbers from 1 to 101 is 2601.
APPEARS IN
RELATED QUESTIONS
In an AP given an = 4, d = 2, Sn = −14, find n and a.
Show that a1, a2,..., an... form an AP where an is defined as below:
an = 9 − 5n
Also, find the sum of the first 15 terms.
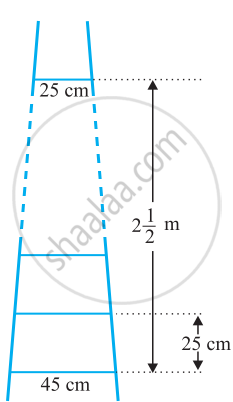
A ladder has rungs 25 cm apart. (See figure). The rungs decrease uniformly in length from 45 cm at the bottom to 25 cm at the top. If the top and bottom rungs are 2 `1/2` m apart, what is the length of the wood required for the rungs?
[Hint: number of rungs = `250/25+ 1`]
How many terms of the A.P. 63, 60, 57, ... must be taken so that their sum is 693?
Find the sum of all odd numbers between 100 and 200.
Determine the A.P. Whose 3rd term is 16 and the 7th term exceeds the 5th term by 12.
The 4th term of an AP is zero. Prove that its 25th term is triple its 11th term.
If 4 times the 4th term of an AP is equal to 18 times its 18th term then find its 22nd term.
Determine k so that (3k -2), (4k – 6) and (k +2) are three consecutive terms of an AP.
If an denotes the nth term of the AP 2, 7, 12, 17, … find the value of (a30 - a20 ).
Kargil’s temperature was recorded in a week from Monday to Saturday. All readings were in A.P. The sum of temperatures of Monday and Saturday was 5°C more than sum of temperatures of Tuesday and Saturday. If temperature of Wednesday was –30° celsius then find the temperature on the other five days.
The A.P. in which 4th term is –15 and 9th term is –30. Find the sum of the first 10 numbers.
The first and the last terms of an A.P. are 8 and 350 respectively. If its common difference is 9, how many terms are there and what is their sum?
Let there be an A.P. with first term 'a', common difference 'd'. If an denotes in nth term and Sn the sum of first n terms, find.
A man is employed to count Rs 10710. He counts at the rate of Rs 180 per minute for half an hour. After this he counts at the rate of Rs 3 less every minute than the preceding minute. Find the time taken by him to count the entire amount.
If S1 is the sum of an arithmetic progression of 'n' odd number of terms and S2 the sum of the terms of the series in odd places, then \[\frac{S_1}{S_2} =\]
Two cars start together in the same direction from the same place. The first car goes at uniform speed of 10 km h–1. The second car goes at a speed of 8 km h–1 in the first hour and thereafter increasing the speed by 0.5 km h–1 each succeeding hour. After how many hours will the two cars meet?
Q.7
Q.12
Find the common difference of an A.P. whose first term is 5 and the sum of first four terms is half the sum of next four terms.
