Advertisements
Advertisements
Question
Show that a1, a2,..., an... form an AP where an is defined as below:
an = 9 − 5n
Also, find the sum of the first 15 terms.
Solution
an = 9 − 5n
a1 = 9 − 5 × 1
= 9 − 5
= 4
a2 = 9 − 5 × 2
= 9 − 10
= −1
a3 = 9 − 5 × 3
= 9 − 15
= −6
a4 = 9 − 5 × 4
= 9 − 20
= −11
It can be observed that
a2 − a1 = −1 − 4 = −5
a3 − a2 = −6 − (−1) = −5
a4 − a3 = −11 − (−6) = −5
i.e., ak + 1 − ak is same every time. Therefore, this is an A.P. with common difference as −5 and first term as 4.
`S_n = n/2 [2a + (n - 1)d]`
`S_15 = 15/2 [2(4) + (15 - 1) (-5)]`
= `15/2 [8 + 14(-5)]`
= `15/2 (8 - 70)`
= `15/2 (-62)`
= 15 × (-31)
= -465
APPEARS IN
RELATED QUESTIONS
Ramkali saved Rs 5 in the first week of a year and then increased her weekly saving by Rs 1.75. If in the nth week, her week, her weekly savings become Rs 20.75, find n.
Find the sum of first 22 terms of an AP in which d = 7 and 22nd term is 149.
Find the sum of first 40 positive integers divisible by 6.
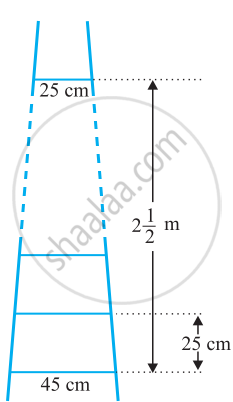
A ladder has rungs 25 cm apart. (See figure). The rungs decrease uniformly in length from 45 cm at the bottom to 25 cm at the top. If the top and bottom rungs are 2 `1/2` m apart, what is the length of the wood required for the rungs?
[Hint: number of rungs = `250/25+ 1`]
Three numbers are in A.P. If the sum of these numbers is 27 and the product 648, find the numbers.
Determine the A.P. Whose 3rd term is 16 and the 7th term exceeds the 5th term by 12.
How many terms of the A.P. : 24, 21, 18, ................ must be taken so that their sum is 78?
The sum of first seven terms of an A.P. is 182. If its 4th and the 17th terms are in the ratio 1 : 5, find the A.P.
Write the sum of first n even natural numbers.
The common difference of the A.P. is \[\frac{1}{2q}, \frac{1 - 2q}{2q}, \frac{1 - 4q}{2q}, . . .\] is
If k, 2k − 1 and 2k + 1 are three consecutive terms of an A.P., the value of k is
A manufacturer of TV sets produces 600 units in the third year and 700 units in the 7th year. Assuming that the production increases uniformly by a fixed number every year, find:
- the production in the first year.
- the production in the 10th year.
- the total production in 7 years.
How many terms of the A.P. 27, 24, 21, …, should be taken so that their sum is zero?
Write the formula of the sum of first n terms for an A.P.
A merchant borrows ₹ 1000 and agrees to repay its interest ₹ 140 with principal in 12 monthly instalments. Each instalment being less than the preceding one by ₹ 10. Find the amount of the first instalment
The sum of all two digit odd numbers is ______.
In an A.P., if Sn = 3n2 + 5n and ak = 164, find the value of k.
Find the sum of last ten terms of the AP: 8, 10, 12,.., 126.
Find the sum of the integers between 100 and 200 that are not divisible by 9.
The sum of the 4th and 8th term of an A.P. is 24 and the sum of the 6th and 10th term of the A.P. is 44. Find the A.P. Also, find the sum of first 25 terms of the A.P.
