Advertisements
Advertisements
Question
Fig shown a block and tackles system of pulleys used to lift a load.

(i) How many strands of tackle are supporting the load?
(ii) Draw arrows to represent tension in each stand.
(iii) What is the mechanical advantage of the system?
(iv) When load is pulled up by a distance 1 m how far does the effort end move?
Solution
(I) 4 stands of tackle are supporting the load.
(ii) correct winding of rope around pulleys, load and effort is as shown:
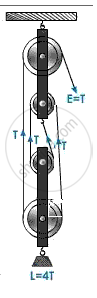
(iii) M .A = L/E
here,L = 4T, E = T
M.A = `(4"T")/"T"` = 4
(iv) since there are four strings in the block and tackle system, therefore, the velocity ratio of the system is V.R = n = 4
Now, V.R `"d"_"E"/"d"_"L"`
or, `"d"_"E" = 4 xx "d"_"L" = 4 xx 1 = 4"m"`
APPEARS IN
RELATED QUESTIONS
A block and tackle system has V.R. = 5.
Draw a neat labeled diagram of a system indicating the direction of its load and effort
Is the above pulley system an ideal machine or not?
Draw a neat labelled diagram showing a pulley being used to lift a load. How are load and effort related in an ideal situation?
State if the following statement is true or false. Correct the statement if it is false.
A single movable pulley is a pulley that has its axis of rotation fixed.
Solve the following numerical problem.
What effort will be required to lift a load of 500 N by a single movable pulley? [Hint: Mechanical advantage of a single movable pulley is two].
Name a machine to change the direction of force ?
Name the type of single pulley that can act as a force multiplier. Draw a labelled diagram of the pulley mentioned by you.
What is a block and tackle system of pulleys?
Draw a diagram showing a block and tackle system of 4 pulleys.

(i) State, how many strands of tackle support the load?
(ii) Draw arrows to represent tension in each strand.
(iii) Find the mechanical advantage of the system, stating the assumptions made.
(iv) If the load is pulled up by a distance 1m, how much does the effort end move?
If the weight of the movable pulley is W, obtain the expression for MA, VR, and efficiency.
