Advertisements
Advertisements
Question
If `veca, vecb, vecc` are mutually perpendicular vectors of equal magnitudes, find the angle which `veca + vecb + vecc`make with `veca or vecb or vecc`
Solution


Thus, angle between `veca` and `veca+vecb+vecc` is `cos^(-1) (1/sqrt3)`
RELATED QUESTIONS
Find a vector `veca` of magnitude `5sqrt2` , making an angle of `π/4` with x-axis, `π/2` with y-axis and an acute angle θ with z-axis.
Find `|veca| and |vecb|`, if `(veca + vecb).(veca -vecb) = 8 and |veca| = 8|vecb|.`
Find the magnitude of two vectors `veca and vecb`, having the same magnitude and such that the angle between them is 60° and their scalar product is `1/2`.
If `veca` is a nonzero vector of magnitude 'a' and λ a nonzero scalar, then λ`veca` is unit vector if ______.
Represent the following graphically:
(i) a displacement of 40 km, 30° east of north
(ii) a displacement of 50 km south-east
(iii) a displacement of 70 km, 40° north of west.
Find the unit vector in the direction of \[3 \hat{i} + 4 \hat{j} - 12 \hat{k} .\]
If the sum of two unit vectors is a unit vector prove that the magnitude of their difference is `sqrt(3)`.
If \[\vec{a} = \hat{i} + \hat{j} + \hat{k} , \vec{b} = 4 \hat{i} - 2 \hat{j} + 3 \hat{k} \text { and } \vec{c} = \hat{i} - 2 \hat{j} + \hat{k} ,\] find a vector of magnitude 6 units which is parallel to the vector \[2 \vec{a} - \vec{b} + 3 \vec{c .}\]
Find a vector \[\vec{r}\] of magnitude \[3\sqrt{2}\] units which makes an angle of \[\frac{\pi}{4}\] and \[\frac{\pi}{4}\] with y and z-axes respectively.
A vector \[\vec{r}\] is inclined at equal angles to the three axes. If the magnitude of \[\vec{r}\] is \[2\sqrt{3}\], find \[\vec{r}\].
Write the length (magnitude) of a vector whose projections on the coordinate axes are 12, 3 and 4 units.
Write a vector in the direction of vector \[5 \hat{i} - \hat{j} + 2 \hat{k}\] which has magnitude of 8 unit.
Find a vector \[\overrightarrow{a}\] of magnitude \[5\sqrt{2}\], making an angle of \[\frac{\pi}{4}\] with x-axis, \[\frac{\pi}{2}\] with y-axis and an acute angle θ with z-axis.
Prove that in a ∆ABC, `sin"A"/"a" = sin"B"/"b" = sin"C"/"c"`, where a, b, c represent the magnitudes of the sides opposite to vertices A, B, C, respectively.
The magnitude of the vector `6hat"i" + 2hat"j" + 3hat"k"` is ______.
Find a vector of magnitude 6, which is perpendicular to both the vectors `2hat"i" - hat"j" + 2hat"k"` and `4hat"i" - hat"j" + 3hat"k"`.
The vector in the direction of the vector `hat"i" - 2hat"j" + 2hat"k"` that has magnitude 9 is ______.
If the sum of two-unit vectors is a unit vector, then the magnitude of their difference is
The area under a velocity-time curve represents the change in ______?
Which of the following statements is false about forces/ couple?
In a triangle ABC three forces of magnitudes `3vec(AB), 2vec(AC)` and `6vec(CB)` are acting along the sides AB, AC and CB respectively. If the resultant meets AC at D, then the ratio DC : AD will be equal to :
The magnitude of the vector `6hati - 2hatj + 3hatk` is ______.
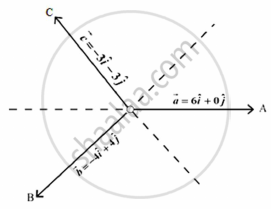
Read the following passage and answer the questions given below:
|
Teams A, B, C went for playing a tug of war game. Teams A, B, C have attached a rope to a metal ring and is trying to pull the ring into their own area. Team A pulls with force F1 = `6hati + 0hatj kN`, Team B pulls with force F2 = `-4hati + 4hatj kN`, Team C pulls with force F3 = `-3hati - 3hatj kN`,
|
- What is the magnitude of the force of Team A ?
- Which team will win the game?
- Find the magnitude of the resultant force exerted by the teams.
OR
In what direction is the ring getting pulled?
Find a vector of magnitude 9 units and perpendicular to the vectors.
`veca = 4hati - hatj + hatk` and `vecb = -2hati + hatj - 2hatk`