Represent the following graphically: (i) a displacement of 40 km, 30° east of north (ii) a displacement of 50 km south-east (iii) a displacement of 70 km, 40° north of west. - Mathematics

Question

Represent the following graphically:
(i) a displacement of 40 km, 30° east of north
(ii) a displacement of 50 km south-east
(iii) a displacement of 70 km, 40° north of west.

Solution

(i) The vector
$\vec{O P}$ represents the required displacement vector.
(ii) The vector
$\vec{O P}$ represents the required vector.
(iii) The vector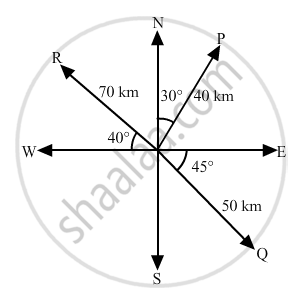
$\vec{O R}$ represents the required vector.

shaalaa.com

Magnitude and Direction of a Vector

Is there an error in this question or solution?

Q 1 Prev Q 2

Chapter 23: Algebra of Vectors - Exercise 23.1 [Page 4]

APPEARS IN

RD Sharma Mathematics [English] Class 12

Chapter 23 Algebra of Vectors
Exercise 23.1 | Q 1 | Page 4

RELATED QUESTIONS

Find $| \vec{a} | and | \vec{b} |$ , if $(\vec{a} + \vec{b}) . (\vec{a} - \vec{b}) = 8 and | \vec{a} | = 8 | \vec{b} | .$

Find the magnitude of two vectors $\vec{a} and \vec{b}$ , having the same magnitude and such that the angle between them is 60° and their scalar product is $\frac{1}{2}$ .

If $\vec{a}$ is a nonzero vector of magnitude 'a' and λ a nonzero scalar, then λ $\vec{a}$ is unit vector if ______.

If $\vec{a}, \vec{b}, \vec{c}$ are mutually perpendicular vectors of equal magnitudes, show that the vector $\vec{a} + \vec{b} + \vec{c}$ is equally inclined to $\vec{a}, \vec{b}$ and $\vec{c}$ .

If $\vec{a}, \vec{b}, \vec{c}$ are mutually perpendicular vectors of equal magnitudes, find the angle which $\vec{a} + \vec{b} + \vec{c}$ make with $\vec{a} or \vec{b} or \vec{c}$

Find the magnitude of the vector $\vec{a} = 2 \hat{i} + 3 \hat{j} - 6 \hat{k} .$

Find the unit vector in the direction of $3 \hat{i} + 4 \hat{j} - 12 \hat{k} .$

Find a vector of magnitude of 5 units parallel to the resultant of the vectors $\vec{a} = 2 \hat{i} + 3 \hat{j} - \hat{k} and \vec{b} = \hat{i} - 2 \hat{j} + \hat{k} .$

Find a vector $\vec{r}$ of magnitude $3 \sqrt{2}$ units which makes an angle of $\frac{π}{4}$ and $\frac{π}{4}$ with y and z-axes respectively.

A vector $\vec{r}$ is inclined at equal angles to the three axes. If the magnitude of $\vec{r}$ is $2 \sqrt{3}$ , find $\vec{r}$ .

Define "zero vector".

Find a vector in the direction of $\vec{a} = 2 \hat{i} - \hat{j} + 2 \hat{k},$ which has magnitude of 6 units.

Find a vector $\vec{a}$ of magnitude $5 \sqrt{2}$ , making an angle of $\frac{π}{4}$ with x-axis, $\frac{π}{2}$ with y-axis and an acute angle θ with z-axis.

If in a ∆ABC, A = (0, 0), B = (3, 3 $\sqrt{3}$ ), C = (−3 $\sqrt{3}$ , 3), then the vector of magnitude 2 $\sqrt{2}$ units directed along AO, where O is the circumcentre of ∆ABC is

Find all vectors of magnitude $10 \sqrt{3}$ that are perpendicular to the plane of $\hat{i} + 2 \hat{j} + \hat{k}$ and $- \hat{i} + 3 \hat{j} + 4 \hat{k}$

The magnitude of the vector $6 \hat{i} + 2 \hat{j} + 3 \hat{k}$ is ______.

A vector $\vec{r}$ is inclined at equal angles to the three axes. If the magnitude of $\vec{r}$ is $2 \sqrt{3}$ units, find $\vec{r}$ .

Find a vector of magnitude 6, which is perpendicular to both the vectors $2 \hat{i} - \hat{j} + 2 \hat{k}$ and $4 \hat{i} - \hat{j} + 3 \hat{k}$ .

Prove that in any triangle ABC, cos A = $\frac{b^{2} + c^{2} - a^{2}}{2 bc}$ , where a, b, c are the magnitudes of the sides opposite to the vertices A, B, C, respectively.

The vector in the direction of the vector $\hat{i} - 2 \hat{j} + 2 \hat{k}$ that has magnitude 9 is ______.

Let $\vec{α} = \hat{i} + 2 \hat{j} - \hat{k}, \vec{β} = 2 \hat{i} - \hat{j} + 3 \hat{k}, \vec{γ} = 2 \hat{i} + \hat{j} + 6 \hat{k}$ . If $\vec{α}$ and $\vec{β}$ are both perpendicular to a vector $\vec{δ}$ and $\vec{δ} . \vec{γ}$ = 10, then the magnitude of $\vec{δ}$ is

If the sum of two-unit vectors is a unit vector, then the magnitude of their difference is

Two equal forces acting at a point with an angle of 60° between them, if the resultant is equal $30 \sqrt{3} N$ , the magnitude of the force will be

Which of the following statements is false about forces/ couple?

In a triangle ABC three forces of magnitudes $3 \vec{A B}, 2 \vec{A C}$ and $6 \vec{C B}$ are acting along the sides AB, AC and CB respectively. If the resultant meets AC at D, then the ratio DC : AD will be equal to :

The magnitude of the vector $6 \hat{i} - 2 \hat{j} + 3 \hat{k}$ is ______.

Read the following passage and answer the questions given below:

Teams A, B, C went for playing a tug of war game. Teams A, B, C have attached a rope to a metal ring and is trying to pull the ring into their own area.

Team A pulls with force F₁ = $6 \hat{i} + 0 \hat{j} k N$ ,

Team B pulls with force F₂ = $- 4 \hat{i} + 4 \hat{j} k N$ ,

Team C pulls with force F₃ = $- 3 \hat{i} - 3 \hat{j} k N$ ,

What is the magnitude of the force of Team A ?
Which team will win the game?
Find the magnitude of the resultant force exerted by the teams.
OR
In what direction is the ring getting pulled?

Represent the following graphically: (i) a displacement of 40 km, 30° east of north (ii) a displacement of 50 km south-east (iii) a displacement of 70 km, 40° north of west. - Mathematics

Advertisements

Advertisements

Question

Solution

APPEARS IN

RELATED QUESTIONS

Select a course

Represent the following graphically: (i) a displacement of 40 km, 30° east of north (ii) a displacement of 50 km south-east (iii) a displacement of 70 km, 40° north of west. - Mathematics

Advertisements

Advertisements

Question

SolutionShow Solution

APPEARS IN

RELATED QUESTIONS

Select a course

Solution