Advertisements
Advertisements
Question
If AB × 4 = 192, then A + B = 7.
Options
True
False
Solution
This statement is False.
Explanation:
AB
We have, × 4
192
Here, B × 4 is a two-digit number whose unit's digit is 2.
Therefore, the value of B is either 3 or 8.
But B = 3 is not possible as A × 4 + 1 ≠ 19 for any value of A between 0 to 9
∴ B = 8 and then A = 4
Hence, A + B = 12
APPEARS IN
RELATED QUESTIONS
Without performing actual addition and division write the quotient when the sum of 69 and 96 is divided by
(i) 11
(ii) 15
Which of the following statement is true?
A number is divisible by 18, if it is divisible by both 3 and 6.
Which of the following statement is true?
If a number is divisible by both 9 and 10, it must be divisible by 90.
Which of the following statement is true?
If a number divides three numbers exactly, it must divide their sum exactly.
If 5A × A = 399, then the value of A is ______.
If 6A × B = A 8 B, then the value of A – B is ______.
If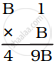 
then B = ______.
A four-digit number abcd is divisible by 11, if d + b = ______ or _____.
If the digit 1 is placed after a 2-digit number whose tens is t and ones digit is u, the new number is ______.
If N ÷ 5 leaves remainder 3 and N ÷ 2 leaves remainder 0, then N ÷ 10 leaves remainder 4.
