Question

If  \[D\left( - \frac{1}{5}, \frac{5}{2} \right), E(7, 3) \text{ and }  F\left( \frac{7}{2}, \frac{7}{2} \right)\]  are the mid-points of sides of  \[∆ ABC\] ,  find the area of  \[∆ ABC\] .

Answer 1

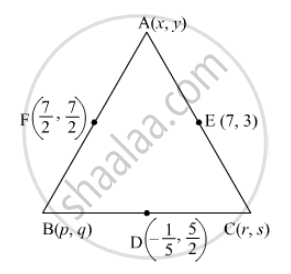
The midpoint of BC is \[D\left( - \frac{1}{5}, \frac{5}{2} \right)\],

The midpoint of AB is \[F\left( \frac{7}{2}, \frac{7}{2} \right)\] ,

The midpoint of AC is \[E\left( 7, 3 \right)\] Consider the line segment BC,

\[\Rightarrow \frac{p + r}{2} = - \frac{1}{2} ; \frac{q + s}{2} = \frac{5}{2}\]
\[ \Rightarrow p + r = - 1 ; q + s = 5 . . . . . (i)\]
\[\text{ Consider the line segment AB, } \]
\[ \Rightarrow \frac{p + x}{2} = \frac{7}{2} ; \frac{q + y}{2} = \frac{7}{2}\]
\[ \Rightarrow p + x = 7 ; q + y = 7 . . . . . (ii)\]

\[\text{ Consider the line segment AC, } \]

\[ \Rightarrow \frac{r + x}{2} = 7 ; \frac{s + y}{2} = 3\]

\[ \Rightarrow r + x = 14 ; s + y = 6 . . . . . (iii)\]

Solve (i), (ii) and (iii) to get

\[A\left( x, y \right) = A\left( 11, 4 \right), B\left( p, q \right) = B\left( - 4, 3 \right), C\left( r, s \right) = C\left( 3, 2 \right)\]

Let us assume that BC is base of the triangle,

 

\[BC = \sqrt{\left( - 4 - 3 \right)^2 + \left( 3 - 2 \right)^2} = \sqrt{50}\]

\[\text{ Equation of the line BC is } \]

\[\frac{x + 4}{- 4 - 3} = \frac{y - 3}{3 - 2}\]

\[ \Rightarrow x + 7y - 17 = 0\]

\[\text{ The perpendicular distance from a point } P\left( x_1 , y_1 \right)is\]

\[P = \left| \frac{1\left( 11 \right) + 7\left( 4 \right) - 17}{\sqrt{50}} \right| = \frac{22}{\sqrt{50}}\]

The area of the triangle is \[A = \frac{1}{2} \times \sqrt{50} \times \frac{22}{\sqrt{50}} = 11 \text{ sq . units } \]