Advertisements
Advertisements
प्रश्न
If \[D\left( - \frac{1}{5}, \frac{5}{2} \right), E(7, 3) \text{ and } F\left( \frac{7}{2}, \frac{7}{2} \right)\] are the mid-points of sides of \[∆ ABC\] , find the area of \[∆ ABC\] .
उत्तर
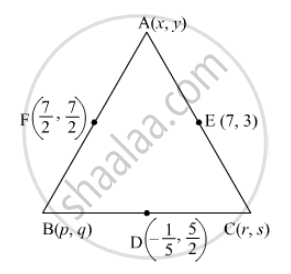
The midpoint of BC is \[D\left( - \frac{1}{5}, \frac{5}{2} \right)\],
The midpoint of AB is \[F\left( \frac{7}{2}, \frac{7}{2} \right)\] ,
The midpoint of AC is \[E\left( 7, 3 \right)\] Consider the line segment BC,
\[ \Rightarrow p + r = - 1 ; q + s = 5 . . . . . (i)\]
\[\text{ Consider the line segment AB, } \]
\[ \Rightarrow \frac{p + x}{2} = \frac{7}{2} ; \frac{q + y}{2} = \frac{7}{2}\]
\[ \Rightarrow p + x = 7 ; q + y = 7 . . . . . (ii)\]
\[\text{ Consider the line segment AC, } \]
\[ \Rightarrow \frac{r + x}{2} = 7 ; \frac{s + y}{2} = 3\]
\[ \Rightarrow r + x = 14 ; s + y = 6 . . . . . (iii)\]
Solve (i), (ii) and (iii) to get
\[BC = \sqrt{\left( - 4 - 3 \right)^2 + \left( 3 - 2 \right)^2} = \sqrt{50}\]
\[\text{ Equation of the line BC is } \]
\[\frac{x + 4}{- 4 - 3} = \frac{y - 3}{3 - 2}\]
\[ \Rightarrow x + 7y - 17 = 0\]
\[\text{ The perpendicular distance from a point } P\left( x_1 , y_1 \right)is\]
\[P = \left| \frac{1\left( 11 \right) + 7\left( 4 \right) - 17}{\sqrt{50}} \right| = \frac{22}{\sqrt{50}}\]
The area of the triangle is \[A = \frac{1}{2} \times \sqrt{50} \times \frac{22}{\sqrt{50}} = 11 \text{ sq . units } \]
APPEARS IN
संबंधित प्रश्न
Find the points of trisection of the line segment joining the points:
5, −6 and (−7, 5),
In what ratio is the line segment joining (-3, -1) and (-8, -9) divided at the point (-5, -21/5)?
If A and B are (1, 4) and (5, 2) respectively, find the coordinates of P when AP/BP = 3/4.
Find the points on the y-axis which is equidistant form the points A(6,5) and B(- 4,3)
Points P, Q, R and S divide the line segment joining the points A(1,2) and B(6,7) in five equal parts. Find the coordinates of the points P,Q and R
Find the area of a quadrilateral ABCD whose vertices area A(3, -1), B(9, -5) C(14, 0) and D(9, 19).
Find the coordinates of the circumcentre of a triangle whose vertices are (–3, 1), (0, –2) and (1, 3).
Points (−4, 0) and (7, 0) lie
If three points (x1, y1) (x2, y2), (x3, y3) lie on the same line, prove that \[\frac{y_2 - y_3}{x_2 x_3} + \frac{y_3 - y_1}{x_3 x_1} + \frac{y_1 - y_2}{x_1 x_2} = 0\]
Write the coordinates of a point on X-axis which is equidistant from the points (−3, 4) and (2, 5).
Write the formula for the area of the triangle having its vertices at (x1, y1), (x2, y2) and (x3, y3).
If x is a positive integer such that the distance between points P (x, 2) and Q (3, −6) is 10 units, then x =
The line segment joining points (−3, −4), and (1, −2) is divided by y-axis in the ratio.
The distance of the point (4, 7) from the y-axis is
The coordinates of a point on x-axis which lies on the perpendicular bisector of the line segment joining the points (7, 6) and (−3, 4) are
Write the equations of the x-axis and y-axis.
Find the point on the y-axis which is equidistant from the points (5, −2) and (−3, 2).
The perpendicular distance of the point P(3, 4) from the y-axis is ______.
The distance of the point (–4, 3) from y-axis is ______.
The distance of the point (–1, 7) from x-axis is ______.
