Question

Find the coordinates of the circumcentre of a triangle whose vertices are (–3, 1), (0, –2) and (1, 3).

Answer 1

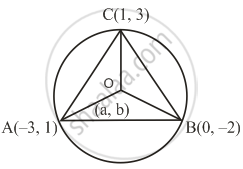
Let A(−3, 1), B(0, −2), C(1, 3) and the circumference O(a, b).

The distance of point O will be equal from A, B and C. 

OA = OC                         ...(Radii of the same circle)

∴ `sqrt([a - (-3)]^2 + (b - 1)^2) = sqrt((a - 1)^2 + (b - 3)^2)`  ...(Distance formula)

Squaring both the sides,

`(a + 3)^2 + (b - 1)^2 = (a - 1)^2 + (b - 3)^2`

`∴ cancela^2 + 6a +cancel9 + cancelb^2 − 2b + cancel1 = cancela^2 − 2a + cancel1 + cancelb^2 − 6b + cancel9`

∴ 6a − 2b = −2a − 6b
∴ 6a + 2a = − 6b + 2b
∴  8a = −4b
∴ 8a + 4b = 0
∴ 4(2a + b) = 0
∴ 2a + b = 0        ....(I)

OB = OC                         ...(Radii of the same circle)
∴ `sqrt((a - 0)^2 + [b - (- 2)]^2) = sqrt((a - 1)^2 + (b - 3)^2)`  ...(Distance formula)

Squaring both the sides,

`(a - 0)^2 + (b + 2)^2 = (a - 1)^2 + (b - 3)^2`

`∴  cancela^2 + cancelb^2 + 4b + 4 = cancela^2 − 2a + 1 + cancelb^2 − 6b + 9`

∴ 4b + 4 = − 2a − 6b + 10
∴ 4b + 2a + 6b = 10 - 4
∴ 2a + 10b = 6          ...(II) 

Subtracting I from II, we get,

\[\begin{array}{1}
\phantom{\texttt{}}\texttt{2a + b = 0}\\ \phantom{\texttt{}}\texttt{- 2a + 10b = 6}\\ \hline\phantom{\texttt{}}\texttt{(-) (-) (-)}\\ \hline \end{array}\]
∴ - 9b = - 6

∴ b = `(-6)/(-9)`

∴ b = `2/3`

Substituting b = `2/3` in equation I, we get,

∴ 2a + b = 0

∴ 2a + `2/3` = 0

∴ 2a = `-2/3`

∴ a = `-2/3 xx 1/2`

∴ a = `(-1)/3`

Coordinates of the circumcentre are `((-1)/3, 2/3)`.