Advertisements
Advertisements
प्रश्न
\[A\left( 6, 1 \right) , B(8, 2) \text{ and } C(9, 4)\] are three vertices of a parallelogram ABCD . If E is the mid-point of DC , find the area of \[∆\] ADE.
उत्तर
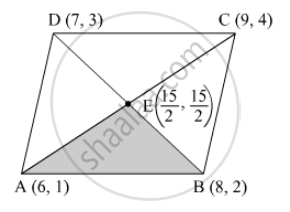
Three vertices are given, then D can be calulated and it comes out to be (7, 3).
Since, E is midpoint of BD.
Therefore, coordinates of E are \[\left( \frac{15}{2}, \frac{5}{2} \right)\] .
Now, vertices of triangle ABE rae (6, 1), (8, 2) and \[\left( \frac{15}{2}, \frac{5}{2} \right)\] .
\[\Rightarrow \text{ Area of the ∆ ABE } = \frac{1}{2}\begin{vmatrix}1 & 6 & 1 \\ 1 & 8 & 2 \\ 1 & \frac{15}{2} & \frac{5}{2}\end{vmatrix}\]
\[ = \frac{1}{2}\left[ 1\left( 20 - 15 \right) - 6\left( \frac{5}{2} - 2 \right) + 1\left( \frac{15}{2} - 8 \right) \right]\]
\[ = \frac{1}{2}\left[ 5 - \frac{6}{2} - \frac{1}{2} \right]\]
\[ = \frac{3}{4} \text{ aq . units } \]
APPEARS IN
संबंधित प्रश्न
Two vertices of an isosceles triangle are (2, 0) and (2, 5). Find the third vertex if the length of the equal sides is 3.
Prove that the points (−2, 5), (0, 1) and (2, −3) are collinear.
Show that the points (−3, 2), (−5,−5), (2, −3) and (4, 4) are the vertices of a rhombus. Find the area of this rhombus.
Find the ratio in which the line segment joining (-2, -3) and (5, 6) is divided by y-axis. Also, find the coordinates of the point of division in each case.
The points A(2, 0), B(9, 1) C(11, 6) and D(4, 4) are the vertices of a quadrilateral ABCD. Determine whether ABCD is a rhombus or not.
Show hat A(1,2), B(4,3),C(6,6) and D(3,5) are the vertices of a parallelogram. Show that ABCD is not rectangle.
Point A lies on the line segment PQ joining P(6, -6) and Q(-4, -1) in such a way that `(PA)/( PQ)=2/5` . If that point A also lies on the line 3x + k( y + 1 ) = 0, find the value of k.
Find the area of the triangle formed by joining the midpoints of the sides of the triangle whose vertices are A(2,1) B(4,3) and C(2,5)
Find the ratio in which the line segment joining the points A(3, 8) and B(–9, 3) is divided by the Y– axis.
Show that `square` ABCD formed by the vertices A(-4,-7), B(-1,2), C(8,5) and D(5,-4) is a rhombus.
A point whose abscissa and ordinate are 2 and −5 respectively, lies in
Find the value of k, if the points A(7, −2), B (5, 1) and C (3, 2k) are collinear.
If the point P (m, 3) lies on the line segment joining the points \[A\left( - \frac{2}{5}, 6 \right)\] and B (2, 8), find the value of m.
If the points A(−2, 1), B(a, b) and C(4, −1) ae collinear and a − b = 1, find the values of aand b.
Write the ratio in which the line segment joining points (2, 3) and (3, −2) is divided by X axis.
If P is a point on x-axis such that its distance from the origin is 3 units, then the coordinates of a point Q on OY such that OP = OQ, are
If A(4, 9), B(2, 3) and C(6, 5) are the vertices of ∆ABC, then the length of median through C is
If segment AB is parallel Y-axis and coordinates of A are (1, 3), then the coordinates of B are ______
Point P(– 4, 2) lies on the line segment joining the points A(– 4, 6) and B(– 4, – 6).
If the perpendicular distance of a point P from the x-axis is 5 units and the foot of the perpendicular lies on the negative direction of x-axis, then the point P has ______.
