Advertisements
Advertisements
Question
\[A\left( 6, 1 \right) , B(8, 2) \text{ and } C(9, 4)\] are three vertices of a parallelogram ABCD . If E is the mid-point of DC , find the area of \[∆\] ADE.
Solution
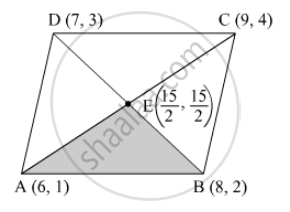
Three vertices are given, then D can be calulated and it comes out to be (7, 3).
Since, E is midpoint of BD.
Therefore, coordinates of E are \[\left( \frac{15}{2}, \frac{5}{2} \right)\] .
Now, vertices of triangle ABE rae (6, 1), (8, 2) and \[\left( \frac{15}{2}, \frac{5}{2} \right)\] .
\[\Rightarrow \text{ Area of the ∆ ABE } = \frac{1}{2}\begin{vmatrix}1 & 6 & 1 \\ 1 & 8 & 2 \\ 1 & \frac{15}{2} & \frac{5}{2}\end{vmatrix}\]
\[ = \frac{1}{2}\left[ 1\left( 20 - 15 \right) - 6\left( \frac{5}{2} - 2 \right) + 1\left( \frac{15}{2} - 8 \right) \right]\]
\[ = \frac{1}{2}\left[ 5 - \frac{6}{2} - \frac{1}{2} \right]\]
\[ = \frac{3}{4} \text{ aq . units } \]
APPEARS IN
RELATED QUESTIONS
Prove that the points (−2, 5), (0, 1) and (2, −3) are collinear.
Find the coordinates of the circumcentre of the triangle whose vertices are (3, 0), (-1, -6) and (4, -1). Also, find its circumradius.
Find a point on the x-axis which is equidistant from the points (7, 6) and (−3, 4).
If the points A (a, -11), B (5, b), C (2, 15) and D (1, 1) are the vertices of a parallelogram ABCD, find the values of a and b.
Determine the ratio in which the point (-6, a) divides the join of A (-3, 1) and B (-8, 9). Also, find the value of a.
Find the points on the y-axis which is equidistant form the points A(6,5) and B(- 4,3)
If the point A (4,3) and B ( x,5) lies on a circle with the centre o (2,3) . Find the value of x.
If the point P (2,2) is equidistant from the points A ( -2,K ) and B( -2K , -3) , find k. Also, find the length of AP.
Find the co-ordinates of the point which divides the join of A(-5, 11) and B(4,-7) in the ratio 7 : 2
In what ratio does the point P(2,5) divide the join of A (8,2) and B(-6, 9)?
Find the ratio in which the pint (-3, k) divide the join of A(-5, -4) and B(-2, 3),Also, find the value of k.
Find the ratio in which the point (-1, y) lying on the line segment joining points A(-3, 10) and (6, -8) divides it. Also, find the value of y.
If the point A(0,2) is equidistant from the points B(3,p) and C(p, 5), find p.
The abscissa of a point is positive in the
If the vertices of a triangle are (1, −3), (4, p) and (−9, 7) and its area is 15 sq. units, find the value(s) of p.
Find the value of k, if the points A(7, −2), B (5, 1) and C (3, 2k) are collinear.
If the mid-point of the segment joining A (x, y + 1) and B (x + 1, y + 2) is C \[\left( \frac{3}{2}, \frac{5}{2} \right)\] , find x, y.
If the area of the triangle formed by the points (x, 2x), (−2, 6) and (3, 1) is 5 square units , then x =
The ratio in which the x-axis divides the segment joining (3, 6) and (12, −3) is
If point P is midpoint of segment joining point A(– 4, 2) and point B(6, 2), then the coordinates of P are ______
