Advertisements
Advertisements
प्रश्न
\[A\left( 6, 1 \right) , B(8, 2) \text{ and } C(9, 4)\] are three vertices of a parallelogram ABCD . If E is the mid-point of DC , find the area of \[∆\] ADE.
उत्तर
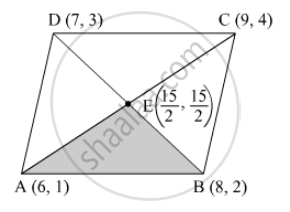
Three vertices are given, then D can be calulated and it comes out to be (7, 3).
Since, E is midpoint of BD.
Therefore, coordinates of E are \[\left( \frac{15}{2}, \frac{5}{2} \right)\] .
Now, vertices of triangle ABE rae (6, 1), (8, 2) and \[\left( \frac{15}{2}, \frac{5}{2} \right)\] .
\[\Rightarrow \text{ Area of the ∆ ABE } = \frac{1}{2}\begin{vmatrix}1 & 6 & 1 \\ 1 & 8 & 2 \\ 1 & \frac{15}{2} & \frac{5}{2}\end{vmatrix}\]
\[ = \frac{1}{2}\left[ 1\left( 20 - 15 \right) - 6\left( \frac{5}{2} - 2 \right) + 1\left( \frac{15}{2} - 8 \right) \right]\]
\[ = \frac{1}{2}\left[ 5 - \frac{6}{2} - \frac{1}{2} \right]\]
\[ = \frac{3}{4} \text{ aq . units } \]
APPEARS IN
संबंधित प्रश्न
Find the ratio in which the line segment joining (-2, -3) and (5, 6) is divided by x-axis Also, find the coordinates of the point of division in each case.
In what ratio does the point (−4, 6) divide the line segment joining the points A(−6, 10) and B(3,−8)?
In what ratio is the line segment joining the points A(-2, -3) and B(3,7) divided by the yaxis? Also, find the coordinates of the point of division.
In what ratio does the point C (4,5) divides the join of A (2,3) and B (7,8) ?
Find the coordinates of the circumcentre of a triangle whose vertices are (–3, 1), (0, –2) and (1, 3).
Point P(x, 4) lies on the line segment joining the points A(−5, 8) and B(4, −10). Find the ratio in which point P divides the line segment AB. Also find the value of x.
Mark the correct alternative in each of the following:
The point of intersect of the coordinate axes is
The abscissa of a point is positive in the
The area of the triangle formed by the points A(2,0) B(6,0) and C(4,6) is
If the points A(−2, 1), B(a, b) and C(4, −1) ae collinear and a − b = 1, find the values of aand b.
Write the coordinates the reflections of points (3, 5) in X and Y -axes.
The area of the triangle formed by (a, b + c), (b, c + a) and (c, a + b)
If the centroid of the triangle formed by (7, x) (y, −6) and (9, 10) is at (6, 3), then (x, y) =
If the line segment joining the points (3, −4), and (1, 2) is trisected at points P (a, −2) and Q \[\left( \frac{5}{3}, b \right)\] , Then,
If A(4, 9), B(2, 3) and C(6, 5) are the vertices of ∆ABC, then the length of median through C is
The distance of the point P(2, 3) from the x-axis is ______.
Point (–3, 5) lies in the ______.
Ordinate of all points on the x-axis is ______.
Find the coordinates of the point which lies on x and y axes both.
If the points P(1, 2), Q(0, 0) and R(x, y) are collinear, then find the relation between x and y.
Given points are P(1, 2), Q(0, 0) and R(x, y).
The given points are collinear, so the area of the triangle formed by them is `square`.
∴ `1/2 |x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2)| = square`
`1/2 |1(square) + 0(square) + x(square)| = square`
`square + square + square` = 0
`square + square` = 0
`square = square`
Hence, the relation between x and y is `square`.
