Advertisements
Advertisements
प्रश्न
Find the value of k, if the points A(7, −2), B (5, 1) and C (3, 2k) are collinear.
उत्तर
The formula for the area ‘A’ encompassed by three points(x1,y1) , (x2 , y2) and (x3 , y3) is given by the formula,
\[∆ = \frac{1}{2}\left| \left( x_1 y_2 + x_2 y_3 + x_3 y_1 \right) - \left( x_2 y_1 + x_3 y_2 + x_1 y_3 \right) \right|\]
If three points are collinear the area encompassed by them is equal to 0.
The three given points are A(7, −2), B(5, 1) and C(3, 2k). It is also said that they are collinear and hence the area enclosed by them should be 0.
\[∆ = \frac{1}{2}\left| \left( 7 \times 1 + 5 \times 2k + 3 \times - 2 \right) - \left( 5 \times - 2 + 3 \times 1 + 7 \times 2k \right) \right|\]
\[ 0 = \frac{1}{2}\left| \left( 7 + 10k - 6 \right) - \left( - 10 + 3 + 14k \right) \right|\]
\[ 0 = \frac{1}{2}\left| - 4k + 8 \right|\]
\[ 0 = - 4k + 8\]
\[ k = 2\]
Hence the value of ‘k’ for which the given points are collinear is k = 2 .
APPEARS IN
संबंधित प्रश्न
If the points A(k + 1, 2k), B(3k, 2k + 3) and C(5k − 1, 5k) are collinear, then find the value of k
On which axis do the following points lie?
P(5, 0)
Let ABCD be a square of side 2a. Find the coordinates of the vertices of this square when A coincides with the origin and AB and AD are along OX and OY respectively.
Find the distance between the following pair of points:
(a, 0) and (0, b)
Find the point on x-axis which is equidistant from the points (−2, 5) and (2,−3).
Find the points on the x-axis, each of which is at a distance of 10 units from the point A(11, –8).
Points P, Q, R and S divide the line segment joining the points A(1,2) and B(6,7) in five equal parts. Find the coordinates of the points P,Q and R
Points P, Q, and R in that order are dividing line segment joining A (1,6) and B(5, -2) in four equal parts. Find the coordinates of P, Q and R.
ABCD is rectangle formed by the points A(-1, -1), B(-1, 4), C(5, 4) and D(5, -1). If P,Q,R and S be the midpoints of AB, BC, CD and DA respectively, Show that PQRS is a rhombus.
Two points having same abscissae but different ordinate lie on
Prove hat the points A (2, 3) B(−2,2) C(−1,−2), and D(3, −1) are the vertices of a square ABCD.
Find the value of k, if the points A (8, 1) B(3, −4) and C(2, k) are collinear.
Write the ratio in which the line segment doining the points A (3, −6), and B (5, 3) is divided by X-axis.
The area of the triangle formed by (a, b + c), (b, c + a) and (c, a + b)
If the points(x, 4) lies on a circle whose centre is at the origin and radius is 5, then x =
If the points P (x, y) is equidistant from A (5, 1) and B (−1, 5), then
The coordinates of a point on x-axis which lies on the perpendicular bisector of the line segment joining the points (7, 6) and (−3, 4) are
Any point on the line y = x is of the form ______.
The distance of the point (3, 5) from x-axis (in units) is ______.
Ryan, from a very young age, was fascinated by the twinkling of stars and the vastness of space. He always dreamt of becoming an astronaut one day. So, he started to sketch his own rocket designs on the graph sheet. One such design is given below :
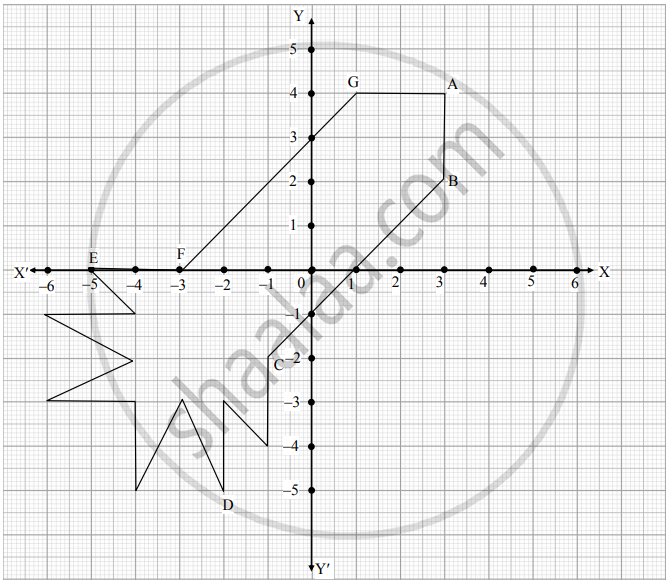
Based on the above, answer the following questions:
i. Find the mid-point of the segment joining F and G. (1)
ii. a. What is the distance between the points A and C? (2)
OR
b. Find the coordinates of the points which divides the line segment joining the points A and B in the ratio 1 : 3 internally. (2)
iii. What are the coordinates of the point D? (1)
