Advertisements
Advertisements
प्रश्न
Find the value of k if points A(k, 3), B(6, −2) and C(−3, 4) are collinear.
उत्तर
The formula for the area ‘A’ encompassed by three points(x1 , y1 ) , (x2 , y2 ) and (x3 , y3 ) is given by the formula,
\[∆ = \frac{1}{2}\left| \left( x_1 y_2 + x_2 y_3 + x_3 y_1 \right) - \left( x_2 y_1 + x_3 y_2 + x_1 y_3 \right) \right|\]
If three points are collinear the area encompassed by them is equal to 0.
The three given points are A(k, 3), B(6, −2) and C(−3, 4). It is also said that they are collinear and hence the area enclosed by them should be 0.
\[∆ = \frac{1}{2}\left| \left( k\left( - 2 \right) + 6 \times 4 + \left( - 3 \right) \times 3 \right) - \left( 6 \times 3 + \left( - 3 \right)\left( - 2 \right) + k \times 4 \right) \right|\]
\[ 0 = \frac{1}{2}\left| \left( - 2k + 24 - 9 \right) - \left( 18 + 6 + 4k \right) \right|\]
\[ 0 = \frac{1}{2}\left| - 2k + 15 - 24 - 4k \right|\]
\[ 0 = \frac{1}{2}\left| - 6k - 9 \right|\]
\[ 0 = - 6k - 9\]
\[ k = - \frac{9}{6} = - \frac{3}{2}\]
Hence the value of ‘k’ for which the given points are collinear is `(k = - 3 /2)`.
APPEARS IN
संबंधित प्रश्न
Prove that the points (3, 0), (6, 4) and (-1, 3) are the vertices of a right-angled isosceles triangle.
The coordinates of the point P are (−3, 2). Find the coordinates of the point Q which lies on the line joining P and origin such that OP = OQ.
Find the value of x such that PQ = QR where the coordinates of P, Q and R are (6, -1), (1, 3) and (x, 8) respectively.
The line segment joining the points P(3, 3) and Q(6, -6) is trisected at the points A and B such that Ais nearer to P. If A also lies on the line given by 2x + y + k = 0, find the value of k.
If A and B are (1, 4) and (5, 2) respectively, find the coordinates of P when AP/BP = 3/4.
Point A lies on the line segment PQ joining P(6, -6) and Q(-4, -1) in such a way that `(PA)/( PQ)=2/5` . If that point A also lies on the line 3x + k( y + 1 ) = 0, find the value of k.
Find the coordinates of the midpoints of the line segment joining
P(-11,-8) and Q(8,-2)
In what ratio is the line segment joining A(2, -3) and B(5, 6) divide by the x-axis? Also, find the coordinates of the pint of division.
ABCD is rectangle formed by the points A(-1, -1), B(-1, 4), C(5, 4) and D(5, -1). If P,Q,R and S be the midpoints of AB, BC, CD and DA respectively, Show that PQRS is a rhombus.
If the point P(k-1, 2) is equidistant from the points A(3,k) and B(k,5), find the value of k.
Show that A(-4, -7), B(-1, 2), C(8, 5) and D(5, -4) are the vertices of a
rhombus ABCD.
If P ( 9a -2 , - b) divides the line segment joining A (3a + 1 , - 3 ) and B (8a, 5) in the ratio 3 : 1 , find the values of a and b .
If (a,b) is the mid-point of the line segment joining the points A (10, - 6) , B (k,4) and a - 2b = 18 , find the value of k and the distance AB.
The points \[A \left( x_1 , y_1 \right) , B\left( x_2 , y_2 \right) , C\left( x_3 , y_3 \right)\] are the vertices of ΔABC .
(i) The median from A meets BC at D . Find the coordinates of the point D.
(ii) Find the coordinates of the point P on AD such that AP : PD = 2 : 1.
(iii) Find the points of coordinates Q and R on medians BE and CF respectively such thatBQ : QE = 2 : 1 and CR : RF = 2 : 1.
(iv) What are the coordinates of the centropid of the triangle ABC ?
The area of the triangle formed by (a, b + c), (b, c + a) and (c, a + b)
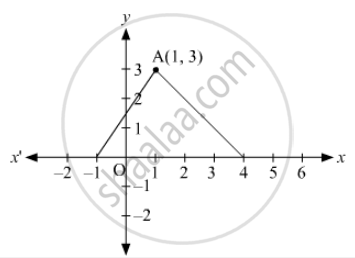
In Fig. 14.46, the area of ΔABC (in square units) is
Find the coordinates of point A, where AB is a diameter of the circle with centre (–2, 2) and B is the point with coordinates (3, 4).
The line segment joining the points (3, -1) and (-6, 5) is trisected. The coordinates of point of trisection are ______.
Point P(– 4, 2) lies on the line segment joining the points A(– 4, 6) and B(– 4, – 6).
Ryan, from a very young age, was fascinated by the twinkling of stars and the vastness of space. He always dreamt of becoming an astronaut one day. So, he started to sketch his own rocket designs on the graph sheet. One such design is given below :
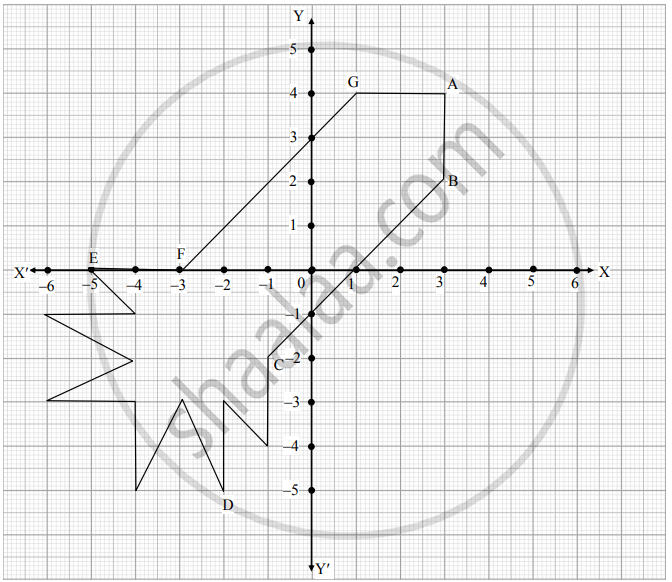
Based on the above, answer the following questions:
i. Find the mid-point of the segment joining F and G. (1)
ii. a. What is the distance between the points A and C? (2)
OR
b. Find the coordinates of the points which divides the line segment joining the points A and B in the ratio 1 : 3 internally. (2)
iii. What are the coordinates of the point D? (1)
