Advertisements
Advertisements
प्रश्न
In what ratio is the line segment joining A(2, -3) and B(5, 6) divide by the x-axis? Also, find the coordinates of the pint of division.
उत्तर
Let AB be divided by the x-axis in the ratio k : 1 at the point P.
Then, by section formula the coordination of P are
`p = ((5k+2)/(k+1),(6k-3)/(k+1))`
But P lies on the x-axis; so, its ordinate is 0.
Therefore , `(6k-3)/(k+1) = 0`
`⇒ 6k -3=0 ⇒ 6k =3 ⇒k = 3/6 ⇒ k = 1/2`
Therefore, the required ratio is `1/2:1 `, which is same as 1 : 2
Thus, the x-axis divides the line AB li the ratio 1 : 2 at the point P.
Applying `k=1/2` we get the coordinates of point.
`p((5k+1)/(k+1) , 0)`
`=p((5xx1/2+2)/(1/2+1),0)`
`= p (((5+4)/2)/((5+2)/2),0)`
`= p (9/3,0)`
= p (3,0)
Hence, the point of intersection of AB and the x-axis is P( 3,0).
APPEARS IN
संबंधित प्रश्न
Prove that the points (−2, 5), (0, 1) and (2, −3) are collinear.
The three vertices of a parallelogram are (3, 4) (3, 8) and (9, 8). Find the fourth vertex.
If two opposite vertices of a square are (5, 4) and (1, −6), find the coordinates of its remaining two vertices.
If (−2, 3), (4, −3) and (4, 5) are the mid-points of the sides of a triangle, find the coordinates of its centroid.
Find the points on the x-axis, each of which is at a distance of 10 units from the point A(11, –8).
ABCD is rectangle formed by the points A(-1, -1), B(-1, 4), C(5, 4) and D(5, -1). If P,Q,R and S be the midpoints of AB, BC, CD and DA respectively, Show that PQRS is a rhombus.
Find the coordinates of the points of trisection of the line segment joining the points (3, –2) and (–3, –4) ?
Show that ΔABC, where A(–2, 0), B(2, 0), C(0, 2) and ΔPQR where P(–4, 0), Q(4, 0), R(0, 2) are similar triangles.
Find the value of k, if the points A (8, 1) B(3, −4) and C(2, k) are collinear.
If the distance between points (x, 0) and (0, 3) is 5, what are the values of x?
Two vertices of a triangle have coordinates (−8, 7) and (9, 4) . If the centroid of the triangle is at the origin, what are the coordinates of the third vertex?
Write the coordinates the reflections of points (3, 5) in X and Y -axes.
If A (1, 2) B (4, 3) and C (6, 6) are the three vertices of a parallelogram ABCD, find the coordinates of fourth vertex D.
The distance between the points (a cos 25°, 0) and (0, a cos 65°) is
If the points (k, 2k), (3k, 3k) and (3, 1) are collinear, then k
If the points P (x, y) is equidistant from A (5, 1) and B (−1, 5), then
What is the form of co-ordinates of a point on the X-axis?
The line 3x + y – 9 = 0 divides the line joining the points (1, 3) and (2, 7) internally in the ratio ______.
Distance of the point (6, 5) from the y-axis is ______.
Ryan, from a very young age, was fascinated by the twinkling of stars and the vastness of space. He always dreamt of becoming an astronaut one day. So, he started to sketch his own rocket designs on the graph sheet. One such design is given below :
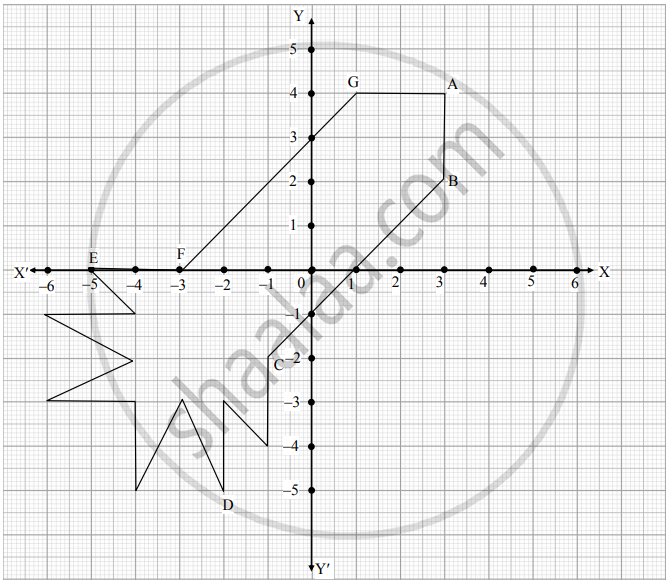
Based on the above, answer the following questions:
i. Find the mid-point of the segment joining F and G. (1)
ii. a. What is the distance between the points A and C? (2)
OR
b. Find the coordinates of the points which divides the line segment joining the points A and B in the ratio 1 : 3 internally. (2)
iii. What are the coordinates of the point D? (1)
