Advertisements
Advertisements
Question
If D is the mid-point of the side BC in ∆ABC where AB = AC, then ∠ADC is ______.
Options
60°
45°
120s°
90°
Solution
If D is the mid-point of the side BC in ∆ABC where AB = AC, then ∠ADC is 90°.
Explanation:
In ∆ABD and ∆ACD,
AD = AD ......[Common]
AB = AC ......[Given]
BD = CD ......[D is the mid-point of BC]
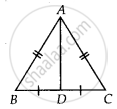
∴ ∆ABD = ∆ACD ......[SSS criterion]
∴ ∠ADB = ∆ADC ......[By C.P.C.T]
But ∠ADB + ∠ADC = 180° ......[∵ BC is a straight line]
⇒ ∠ADC + ∠ADC = 180°
⇒ 2∠ADC = 180°
⇒ ∠ADC = 90°
APPEARS IN
RELATED QUESTIONS
Consider the given pairs of triangles and say whether each pair is that of congruent triangles. If the triangles are congruent, say ‘how’; if they are not congruent say ‘why’ and also say if a small modification would make them congruent: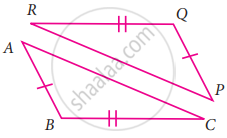
Consider the given pairs of triangles and say whether each pair is that of congruent triangles. If the triangles are congruent, say ‘how’; if they are not congruent say ‘why’ and also say if a small modification would make them congruent:
To conclude the congruency of triangles, mark the required information in the following figure with reference to the given congruency criterion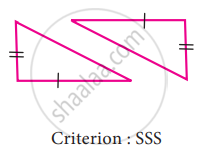
Construct a triangle XYZ with the given conditions.
XY = 6.4 cm, ZY = 7.7 cm and XZ = 5 cm
Construct a triangle XYZ with the given conditions.
An equilateral triangle of side 7.5 cm
In the given figure FG = FI and H is midpoint of GI, prove that ∆FGH ≅ ∆FHI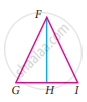
In the following pairs of triangles of figure, the lengths of the sides are indicated along the sides. By applying SSS congruence criterion, determine which triangles are congruent. If congruent, write the results in symbolic form.
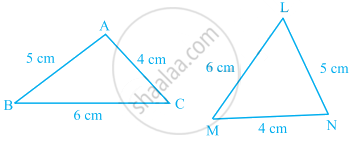
In the following pairs of triangles of figure, the lengths of the sides are indicated along the sides. By applying SSS congruence criterion, determine which triangles are congruent. If congruent, write the results in symbolic form.
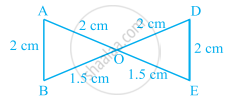
In the following pairs of triangles of figure, the lengths of the sides are indicated along the sides. By applying SSS congruence criterion, determine which triangles are congruent. If congruent, write the results in symbolic form.
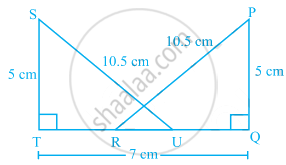
If ΔPQR and ΔSOR are both isosceles triangle on a common base OR such that P and S lie on the same side of QR. Are triangles PSQ and PSR congruent? Which condition do you use?
