Advertisements
Advertisements
Question
If K = {a, b, d, e, f}, L = {b, c, d, g} and M = {a, b, c, d, h} then find the following:
(K ∪ L) ∩ (K ∪ M)
Solution
K = {a, b, d, e, f}, L = {b, c, d, g} and M = {a, b, c, d, h}
(K ∪ L) ∩ (K ∪ M)
(K ∪ L) = {a, b, d, e, f} ∪ {b, c, d, g}
= {a, b, c, d, e, f, g}
(K ∪ M) = {a, b, d, e, f} ∪ {a, b, c, d, h}
= {a, b, c, d, e, f, h}
(K ∪ L) ∩ (K ∪ M) = {a, b, c, d, e, f, g} ∩ {a, b, c, d, e, f, h}
= {a, b, c, d, e, f}
APPEARS IN
RELATED QUESTIONS
Using the adjacent Venn diagram, find the following set:
A – B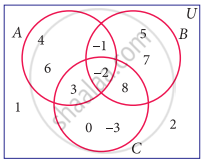
Using the adjacent Venn diagram, find the following set:
A’ ∪ B’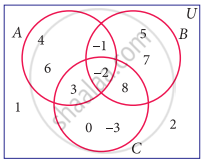
Using the adjacent Venn diagram, find the following set:
A’ ∩ B’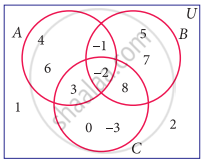
Using the adjacent Venn diagram, find the following set:
A – (B ∪ C)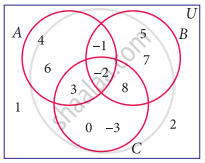
If K = {a, b, d, e, f}, L = {b, c, d, g} and M = {a, b, c, d, h} then find the following:
K ∪ (L ∩ M)
If K = {a, b, d, e, f}, L = {b, c, d, g} and M = {a, b, c, d, h} then find the following:
K ∩ (L ∪ M)
Verify A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C) using Venn diagrams
If A = {x : x = 6n, n ∈ W and n < 6}, B = {x : x = 2n, n ∈ N and 2 < n ≤ 9} and C = {x : x = 3n, n ∈ N and 4 ≤ n < 10}, then show that A – (B ∩ C) = (A – B) ∪ (A – C)
If A = `{y : y = ("a"+1)/2, "a" ∈ "W" and "a" ≤ 5}`, B = `{y : y = (2"n" – 1)/2, "n" ∈ "W" and "n" < 5}` and C = `{-1, −1/2, 1, 3/2, 2}` then show that A – (B ∪ C) = (A – B) ∩ (A – C)
Verify (A ∩ B)’ = A’ ∪ B’ using Venn diagrams
