Advertisements
Advertisements
Question
If p is length of perpendicular from origin to the line whose intercepts on the axes are a and b, then show that `1/("p"^3) = 1/("a"^2) + 1/("b"^2)`
Solution
The equation of the line with x-intercept a and y-intercept b is `x/"a" + y/"b"` = 1 ......(1)
The length of the perpendicular from the origin (0, 0) to the line (1) is
p = `(1/"a" xx 0 + 1/"b" xx 0 - 1)/sqrt((1/"a")^2 + (1/"b")^2`
p = `- 1/sqrt(1/("a"^2) + 1/("b"^2)`
Since p is the length p cannot be negative.
∴ p = `1/sqrt(1/("a"^2) + 1/("b"^2)`
`1/"p" = sqrt(1/("a"^2) + 1/("b"^2)`
Squaring on both sides
`1/("p"^2) = 1/("a"^2) + 1/("b"^2)`
APPEARS IN
RELATED QUESTIONS
Find the acute angle between the X-axis and the line joining points A(3, −1) and B(4, −2).
Select the correct option from the given alternatives:
The angle between the line `sqrt(3)x - y - 2` = 0 and `x - sqrt(3)y + 1` = 0 is
Answer the following question:
Find the value of k the points A(1, 3), B(4, 1), C(3, k) are collinear
Answer the following question:
Line through A(h, 3) and B(4, 1) intersect the line 7x − 9y − 19 = 0 at right angle Find the value of h
The normal boiling point of water is 100°C or 212°F and the freezing point of water is 0°C or 32°F. Find the linear relationship between C and F
An object was launched from a place P in constant speed to hit a target. At the 15th second, it was 1400 m from the target, and at the 18th second 800 m away. Find the distance covered by it in 15 seconds
An object was launched from a place P in constant speed to hit a target. At the 15th second, it was 1400 m from the target, and at the 18th second 800 m away. Find time taken to hit the target
Population of a city in the years 2005 and 2010 are 1,35,000 and 1,45,000 respectively. Find the approximate population in the year 2015. (assuming that the growth of population is constant)
Find the equation of the straight lines passing through (8, 3) and having intercepts whose sum is 1
Show that the points (1, 3), (2, 1) and `(1/2, 4)` are collinear, by using concept of slope
A straight line is passing through the point A(1, 2) with slope `5/12`. Find points on the line which are 13 units away from A
A 150 m long train is moving with constant velocity of 12.5 m/s. Find time taken to cross a pole
A 150 m long train is moving with constant velocity of 12.5 m/s. Find time taken to cross the bridge of length 850 m
A spring was hung from a hook in the ceiling. A number of different weights were attached to the spring to make it stretch, and the total length of the spring was measured each time is shown in the following table
| Weight (kg) | 2 | 4 | 5 | 8 |
| Length (cm) | 3 | 4 | 4.5 | 6 |
Find the equation relating the length of the spring to the weight on it
A spring was hung from a hook in the ceiling. A number of different weights were attached to the spring to make it stretch, and the total length of the spring was measured each time is shown in the following table
| Weight (kg) | 2 | 4 | 5 | 8 |
| Length (cm) | 3 | 4 | 4.5 | 6 |
What is the actual length of the spring
In a shopping mall there is a hall of cuboid shape with dimension 800 × 800 × 720 units, which needs to be added the facility of an escalator in the path as shown by the dotted line in the figure. Find the minimum total length of the escalator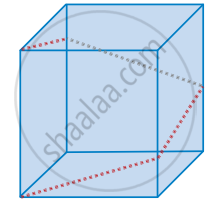
In a shopping mall there is a hall of cuboid shape with dimension 800 × 800 × 720 units, which needs to be added the facility of an escalator in the path as shown by the dotted line in the figure. Find the heights at which the escalator changes its direction
Choose the correct alternative:
Straight line joining the points (2, 3) and (−1, 4) passes through the point (α, β) if
The number of possible tangents which can be drawn to the curve 4x2 – 9y2 = 36, which are perpendicular to the straight line 5x + 2y – 10 = 0 is ______.
Find the coordinates of the point which divides the line segment joining the points (1, –2, 3) and (3, 4, –5) internally in the ratio 2 : 3.
