Advertisements
Advertisements
Question
If the sum of three consecutive terms of an increasing A.P. is 51 and the product of the first and third of these terms is 273, then the third term is
Options
13
9
21
17
Solution
In the given problem, the sum of three consecutive terms of an A.P is 51 and the product of the first and the third terms is 273.
We need to find the third term.
Here,
Let the three terms be (a-d),a,(a + d) where, a is the first term and d is the common difference of the A.P
So,
(a - d) + a + ( a + d) = 51
3a = 51
`a = 51/3`
a = 17
Also,
( a - d) ( a + d ) = 273
a2 - d2 = 273 [ Using a2 - d2 = (a + b ) (a - b)]
172 - d2 = 273
289 - d2 = 273
Further solving for d,
Now, it is given that this is an increasing A.P. so d cannot be negative.
So, d = 4
Substituting the values of a and d in the expression for the third term, we get,
Third term = a + d
So,
a + d = 17 + 4
= 21
Therefore, the third term is a3 = 21
APPEARS IN
RELATED QUESTIONS
Find the 9th term from the end (towards the first term) of the A.P. 5, 9, 13, ...., 185
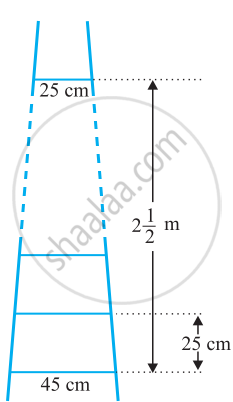
A ladder has rungs 25 cm apart. (See figure). The rungs decrease uniformly in length from 45 cm at the bottom to 25 cm at the top. If the top and bottom rungs are 2 `1/2` m apart, what is the length of the wood required for the rungs?
[Hint: number of rungs = `250/25+ 1`]
Find how many integers between 200 and 500 are divisible by 8.
Which term of the AP 21, 18, 15, …… is -81?
In an A.P. sum of three consecutive terms is 27 and their product is 504, find the terms.
(Assume that three consecutive terms in A.P. are a – d, a, a + d).
Choose the correct alternative answer for the following question.
For an given A.P. a = 3.5, d = 0, n = 101, then tn = ....
Simplify `sqrt(50)`
Obtain the sum of the first 56 terms of an A.P. whose 18th and 39th terms are 52 and 148 respectively.
For an A.P., If t1 = 1 and tn = 149 then find Sn.
Activitry :- Here t1= 1, tn = 149, Sn = ?
Sn = `"n"/2 (square + square)`
= `"n"/2 xx square`
= `square` n, where n = 75
In a ‘Mahila Bachat Gat’, Kavita invested from the first day of month ₹ 20 on first day, ₹ 40 on second day and ₹ 60 on third day. If she saves like this, then what would be her total savings in the month of February 2020?
