Advertisements
Advertisements
Question
If the coordinates of the mid-points of the sides AB, BC and CA of a triangle are (3, 4), (1, 1) and (2, −3) respectively, then the vertices A and B of the triangle are
Options
(3, 2), (2, 4)
(4, 0), (2, 8)
(3, 4), (2, 0)
(4, 3), (2, 4)
Solution
(4, 0), (2, 8)
Explanation;
Hint: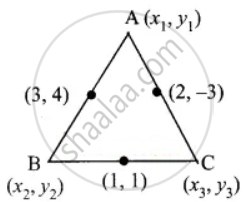
x1 + x2 = 6 → (1)
y1 + y2 = 8 → (2)
x2 + x3 = 2 → (3)
y2 + y3 = 2 → (4)
x1 + x3 = 4 → (5)
y1 + y3 = −6 → (6)
Adding (1) + (3) + (5) we get,
2(x1 + x2 + x3) = 3
x1 + x2 + x3 = 6
x1 + x3 = 4
∴ x2 = 6 – 4 = 2
x2 + x3 = 2
x1 = 6 – 2 = 4
Adding (2) + (4) + (6) we get,
2(y1 + y2 + y3) = 4
y1 + y2 + y3 = 2
y2 + y3 = 2
∴ y1 = 2 – 2 = 0
y1 + y3 = −6
y2 = 2 + 6 = 8
∴ The vertices A is (4, 0) and B is (2, 8).
APPEARS IN
RELATED QUESTIONS
Find the coordinates of the point which divides the line segment joining the points A(4, −3) and B(9, 7) in the ratio 3 : 2
In what ratio does the point P(2, −5) divide the line segment joining A(−3, 5) and B(4, −9)
Find the coordinates of a point P on the line segment joining A(1, 2) and B(6, 7) in such a way that AP = `2/5` AB
Find the coordinates of the points of trisection of the line segment joining the points A(−5, 6) and B(4, −3)
The line segment joining A(6, 3) and B(−1, −4) is doubled in length by adding half of AB to each end. Find the coordinates of the new end points.
A line segment AB is increased along its length by 25% by producing it to C on the side of B. If A and B have the coordinates (−2, −3) and (2, 1) respectively, then find the coordinates of C.
