Advertisements
Advertisements
Question
If x + 5 is the mean proportional between x + 2 and x + 9; find the value of x.
Solution
Given, x + 5 is the mean proportional between x + 2 and x + 9.
`\implies` (x + 2), (x + 5) and (x + 9) are in continued proportion.
`\implies` (x + 2) : (x + 5) = (x + 5) : (x + 9)
`\implies` (x + 5)2 = (x + 2)(x + 9)
`\implies` x2 + 25 + 10x = x2 + 2x + 9x + 18
`\implies` 25 – 18 = 11x – 10x
`\implies` x = 7
APPEARS IN
RELATED QUESTIONS
Find two numbers such that the mean proportional between them is 12 and the third proportional to them is 96.
Using properties of proportion, solve for x:
`(sqrt(x + 5) + sqrt(x - 16))/(sqrt(x + 5) - sqrt(x - 16)) = 7/3`
Given four quantities p, q, r and s are in proportion, show that
q2(p - r) : rs (q - s) =(p2- q2- pq): ( r2-s2-rs).
Find the two numbers such that their mean proprtional is 24 and the third proportinal is 1,536.
If a, b, c and d are in proportion, prove that: `abcd [(1/a^2 + 1/b^2 + 1/c^2 + 1/d^2]` = a2 + b2 + c2 + d2
If a, b, c are in continued proportion, prove that: `(a + b)/(b + c) = (a^2(b - c))/(b^2(a - b)`.
If a, b, c are in continued proportion, prove that: (a + b + c) (a – b + c) = a2 + b2 + c2
Find whether 12, 24, 18, 36 are in order that can be expressed as two ratios that are in proportion
Unequal masses will not balance on a fulcrum if they are at equal distance from it; one side will go up and the other side will go down.
Unequal masses will balance when the following proportion is true:
`("mass"1)/("length"2) = ("mass"2)/("length"1)`
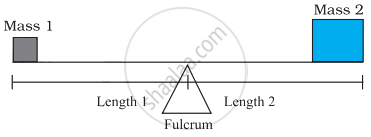
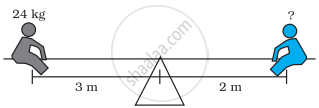
Two children can be balanced on a seesaw when
`("mass"1)/("length"2) = ("mass"2)/("length"1)`. The child on the left and child on the right are balanced. What is the mass of the child on the right?
Are the following statements true?
45 km : 60 km = 12 hours : 15 hours
