Advertisements
Advertisements
Question
Given four quantities p, q, r and s are in proportion, show that
q2(p - r) : rs (q - s) =(p2- q2- pq): ( r2-s2-rs).
Solution
p, q, r and s are 1n proportion
then, p : q :: r : s
Let `"p"/"q" = "r"/"s" = "k"`
Then p = kq and r =ks
Now, we have to prove that
`(("p" - "r")"q"^2)/(("q - s")"rs") = ("p"^2 - "q"^2 - "pq")/("r"^2 - "s"^2 - "rs")`
LHS
`= (("p" - "r")"q"^2)/(("q - s")"rs")`
`= (("kq" - "ks")"q"^2)/(("q - s")"ks" xx "s")`
`= ("k"("q - s")"q"^2)/("ks"^2 ("q - s"))`
`= "q"^2/"s"^2`
RHS
`= ("p"^2 - "q"^2 - "pq")/("r"^2 - "s"^2 - "rs")`
`= ("k"^2"q"^2 - "q"^2 - "kq" xx "q")/("k"^2"s"^2 - "s"^2 - "ks" xx "s")`
`= ("q"^2("k"^2 - 1 - "k"))/("s"^2("k"^2 - 1 - "k"))`
`= "q"^2/"s"^2`
LHS = RHS
APPEARS IN
RELATED QUESTIONS
If q is the mean proportional between p and r prove that `(p^3 + q^3 + r^3)/(p^2q^2r^2) = 1/p^3 + 1/q^3 = 1/r^3`
If x, y, z are in continued proportion prove that `(x + y)^2/(y + z)^2 = x/z`
Find the fourth proportion to the following :
(x2 - y2),(x3 + y3)anc(x3 - xy2 + x2y- y3)
If q is the mean proportional between p and r, prove that
`p^2 - q^2 + r^2 = q^4[(1)/p^2 - (1)/q^2 + (1)/r^2]`.
Determine if the following numbers are in proportion:
150, 200, 250, 300
The cost of 18 chairs is Rs 22770. How many such chairs can be bought for Rs 10120?
If a, b, c, d, e are in continued proportion, prove that: a : e = a4 : b4.
Fill the boxes using any set of suitable numbers 6 : `square` : : `square` : 15
Unequal masses will not balance on a fulcrum if they are at equal distance from it; one side will go up and the other side will go down.
Unequal masses will balance when the following proportion is true:
`("mass"1)/("length"2) = ("mass"2)/("length"1)`
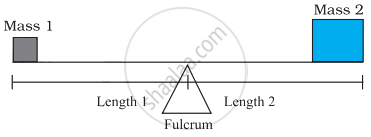
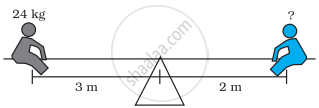
Two children can be balanced on a seesaw when
`("mass"1)/("length"2) = ("mass"2)/("length"1)`. The child on the left and child on the right are balanced. What is the mass of the child on the right?
If x + y + z = 0, the value of `x/(y + z)` is ______.
