Advertisements
Advertisements
Question
Illustrate-combination of cells e.g., three cells, in parallel, explaining the combination briefly. Obtain an expression for current ‘i’ in the combination.
Solution
Combination of cells in parallel: Let there be n cells, each of e.m.f. E and internal resistance r, be connected in parallel as shown in the diagram.
Total e.m.f. across the point A and B is E
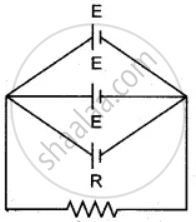
Total internal resistance
`1/"r"_1 = 1/"r" + 1/"r" + 1/"r".... = "n"/"r"` (if there are n cells)
or r1 = `"r"/"n"`
But total resistance of circuit = R + `"r"/"n" = ("nR" + "r")/"n"`
∴ Current i = `"Total e.m.f"/"Total resistance"`
`= "E"/("R" + "r"/"n")`
`= "nE"/("nR + "r"")`
It is advantageous to join cells in parallel when the internal resistance of each cell is quite high as compared to the external resistance R.
Then, Approximately, i = `"nE"/"r"` (neglecting R).
APPEARS IN
RELATED QUESTIONS
What is (a) highest, and (b)Ω lowest, resistance which can be obtained by combining four resistors having the following resistances?
4 Ω, 8 Ω, 12 Ω, 24 Ω
You have three resistors of values 2 `Omega`, 3 `Omega`, and 5 `Omega`. How will you join them so that the total resistance is less than 2 `Omega`?
Write an expression for the resistance of a conducting wire in terms of its length and area of cross-section.
State expression for Cells connected in parallel.
Two lamps of resistance 30Ω and 20Ω respectively are connected in series in a 110V circuit. Calculate:
(i) the total resistance in the circuit
(ii) the current in the circuit, and
(iii) the voltage drop across each lamp.
2Ω resistor A, 1Ω resistor B and 4Ω resistor C are connected in parallel. The combination is connected across a 2V battery of negligible resistance. Draw the diagram of the arrangement and calculate:
(i) The current in each resistor A and C,
(ii) The current through battery.
Two resistors having 2Ω and 3Ω resistance are connected—(i) in series, and (ii) in parallel. Find the equivalent resistance in each case.
When a 4 Ω resistor is connected across the terminals of a 2 V battery, the number of coulombs passing through the resistor per second is:
