Advertisements
Advertisements
Question
In a pentagon PQRST, ∠P = 100°, ∠Q = 120° and ∠S = ∠T. The sides PQ and SR, when produced meet at right angle. Find ∠QRS and ∠PTS.
Solution
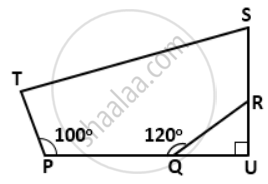
In the figure, PQ and SR produced meet at point P,
∴ ∠U = 90°
∠Q = 120°
⇒∠UQR = 180° - 120° = 60°
∴ ∠URQ = 90° - ∠UQR = 90° - 60° = 30°
∴ QRS = 180° - ∠URQ = 180° - 30° = 150°
Let ∠S = ∠T = x
Since, ∠P + ∠Q + ∠QRS + ∠S + ∠T = (5 - 2) x 180°
⇒100° + 120° + 150° + x + x = 3 x 180°
⇒370° + 2x = 540°
⇒ 2x = 170°
⇒ x = 85°
HEnce, ∠PTS = 85°.
APPEARS IN
RELATED QUESTIONS
One angle of a six-sided polygon is 140o and the other angles are equal.
Find the measure of each equal angle.
AB, BC, and CD are the three consecutive sides of a regular polygon. If BAC = 15°;
Find:
- Each interior angle of the polygon.
- Each exterior angle of the polygon.
- The number of sides of the polygon.
In a pentagon ABCDE, AB is parallel to DC and ∠A: ∠E : ∠D = 3: 4: 5. Find angle E.
Find the number of sides in a regular polygon, when each interior angle is: 140°
Find the number of sides in a regular polygon, when each exterior angle is: 60°
Find the number of sides in a regular polygon, when each exterior angle is: 72°
Is it possible to have a polygon whose each interior angle is 124°?
KL, LM and MN are three consecutive sides of a regular polygon. If ∠LKM = 20°, find the interior angle of the polygon and the number of sides of the polygon.
The sum of the interior angles of a polygon is 6.5 times the sum of its exterior angles. Find the number of sides of the polygon.
The difference between an exterior angle of (n - 1) sided regular polygon and an exterior angle of (n + 2) sided regular polygon is 6°. Find the value of n.
