Advertisements
Advertisements
Question
In a hexagon JKLMNO, side JK || ON and ∠K : ∠L : ∠M : ∠N = 6 : 5 : 4 : 3. Find the angle ∠K and ∠M.
Solution
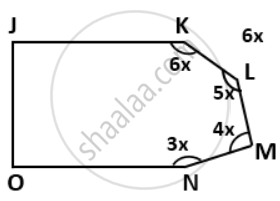
Given JK || ON
⇒ ∠J + ∠O = 180°
Also, ∠K : ∠L : ∠M : ∠N = 6 : 5 : 4 : 3
⇒ ∠K = 6x, ∠L = 5x, ∠M = 4x and ∠N = 3x
Since, ∠J + ∠K + ∠L + ∠M +∠N = 4 x 180°
⇒ (∠J + ∠O) +∠K + ∠L + ∠M + ∠N = 4 x 180°
⇒180° + 6x + 5x + 4x + 3x = 720°
⇒ 18x + 180° = 720°
⇒18x = 540°
⇒ x = 30°
Hence,
∠K = 6x
= 6 x 30°
= 180°
and
∠M = 4x
= 4 x 30°
= 120°.
APPEARS IN
RELATED QUESTIONS
Two alternate sides of a regular polygon, when produced, meet at the right angle.
Find:
(i)The value of each exterior angle of the polygon;
(ii) The number of sides in the polygon.
In a polygon, there are 5 right angles and the remaining angles are equal to 195o each. Find the number of sides in the polygon.
Find the sum of the interior angles of a polygon of: 9 sides
Find each exterior angle of a regular polygon of: 9 sides
Find the number of sides in a regular polygon, when each interior angle is: 140°
Is it possible to have a polygon whose sum of interior angles is 780°?
A heptagon has three angles equal to 120°, and the other four angles are equal. Find all the angles.
Find the value of each angle of a heptagon If three of its angles measure 132° each and the remaining four.
The sum of the interior angles of a polygon is 6.5 times the sum of its exterior angles. Find the number of sides of the polygon.
Each interior angle of a regular polygon is 162°. Another regular polygon has number of sides double the first polygon. Find each interior angle of the second polygon.
