Advertisements
Advertisements
Question
In a regular pentagon PQRST, PR = QT intersect at N. Find the angle RQT and QNP.
Solution
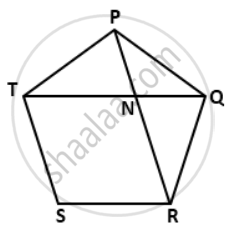
Each interior angle of a regular pentagon
= `((5 - 2) xx 180°)/(5)`
= 3 x 36°
= 108°
Now, In ΔPQT,
⇒ PT = PQ ....(sides of a regular pentagon)
∠PQT = ∠PTQ = x(say)
Now, ∠QT + ∠{TQ +∠QPT = 180°
⇒ x + x + 108° = 180°
⇒ 2x = 72°
⇒ x = 36°
⇒ ∠PQT = ∠PTQ = 36°
Similarly, we can prove that in ΔPQR,
∠QPR = ∠QRP = 36°
Now, ∠RQT
= ∠RQP -∠PQT
= 108° - 36°
= 72°
In ΔQNP,
∠PQN +∠QPN + ∠QNP = 180°
⇒ 36° + 36° + ∠QNP = 180°
⇒ ∠QNP = 180° - 72°
⇒ ∠ QNP = 108°.
APPEARS IN
RELATED QUESTIONS
The sum of the interior angles of a polygon is four times the sum of its exterior angles.
Find the number of sides in the polygon.
AB, BC, and CD are the three consecutive sides of a regular polygon. If BAC = 15°;
Find:
- Each interior angle of the polygon.
- Each exterior angle of the polygon.
- The number of sides of the polygon.
In a parallelogram ABCD, AB = 20 cm and AD = 12 cm. The bisector of angle A meets DC at E and BC produced at F.
Find the length of CF.
Find the measure of each interior angle of a regular polygon of: 10 sides
Find each exterior angle of a regular polygon of: 9 sides
Find each exterior angle of a regular polygon of: 18 sides
Calculate the measure of each angle of a regular polygon of 20 sides.
Is it possible to have a polygon whose each interior angle is 105°?
Find the value of each angle of an octagon if two of its angles are 148° and 152° and the remaining angles are all equal.
In a pentagon PQRST, ∠P = 100°, ∠Q = 120° and ∠S = ∠T. The sides PQ and SR, when produced meet at right angle. Find ∠QRS and ∠PTS.
