Advertisements
Advertisements
प्रश्न
In a regular pentagon PQRST, PR = QT intersect at N. Find the angle RQT and QNP.
उत्तर
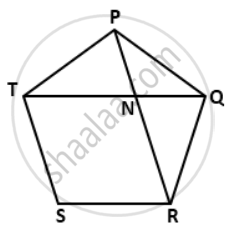
Each interior angle of a regular pentagon
= `((5 - 2) xx 180°)/(5)`
= 3 x 36°
= 108°
Now, In ΔPQT,
⇒ PT = PQ ....(sides of a regular pentagon)
∠PQT = ∠PTQ = x(say)
Now, ∠QT + ∠{TQ +∠QPT = 180°
⇒ x + x + 108° = 180°
⇒ 2x = 72°
⇒ x = 36°
⇒ ∠PQT = ∠PTQ = 36°
Similarly, we can prove that in ΔPQR,
∠QPR = ∠QRP = 36°
Now, ∠RQT
= ∠RQP -∠PQT
= 108° - 36°
= 72°
In ΔQNP,
∠PQN +∠QPN + ∠QNP = 180°
⇒ 36° + 36° + ∠QNP = 180°
⇒ ∠QNP = 180° - 72°
⇒ ∠ QNP = 108°.
APPEARS IN
संबंधित प्रश्न
One angle of a six-sided polygon is 140o and the other angles are equal.
Find the measure of each equal angle.
In a pentagon ABCDE, AB is parallel to DC and ∠A: ∠E : ∠D = 3: 4: 5. Find angle E.
Find each exterior angle of a regular polygon of: 15 sides
Find the number of sides in a regular polygon, when each interior angle is: 120°
Is it possible to have a polygon whose sum of interior angles is 7 right angles?
A heptagon has three angles equal to 120°, and the other four angles are equal. Find all the angles.
The number of sides of two regular polygons are in the ratio 2 : 3 and their interior angles are in the ratio 9 : 10. Find the number of sides of each polygon.
KL, LM and MN are three consecutive sides of a regular polygon. If ∠LKM = 20°, find the interior angle of the polygon and the number of sides of the polygon.
The number angle of a regular polygon is double the exterior angle. Find the number of sides of the polygon.
Each exterior angle of a regular polygon is `(1)/"P" `times of its interior angle. Find the number of sides in the polygon.
